Nyström Subspace Learning for Large-scale SVMs

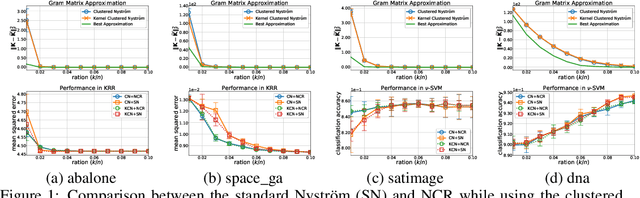
As an implementation of the Nystr\"{o}m method, Nystr\"{o}m computational regularization (NCR) imposed on kernel classification and kernel ridge regression has proven capable of achieving optimal bounds in the large-scale statistical learning setting, while enjoying much better time complexity. In this study, we propose a Nystr\"{o}m subspace learning (NSL) framework to reveal that all you need for employing the Nystr\"{o}m method, including NCR, upon any kernel SVM is to use the efficient off-the-shelf linear SVM solvers as a black box. Based on our analysis, the bounds developed for the Nystr\"{o}m method are linked to NSL, and the analytical difference between two distinct implementations of the Nystr\"{o}m method is clearly presented. Besides, NSL also leads to sharper theoretical results for the clustered Nystr\"{o}m method. Finally, both regression and classification tasks are performed to compare two implementations of the Nystr\"{o}m method.