NTopo: Mesh-free Topology Optimization using Implicit Neural Representations
Paper and Code
Feb 22, 2021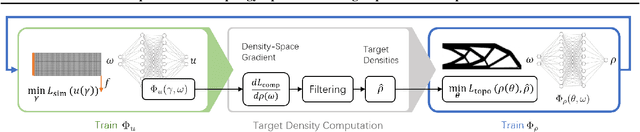
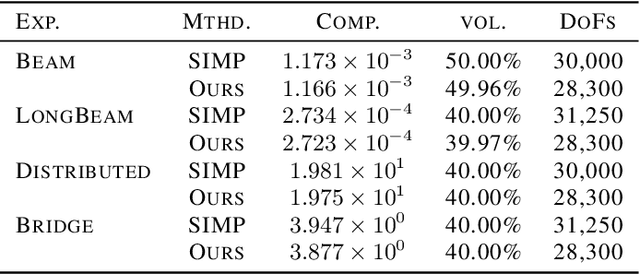
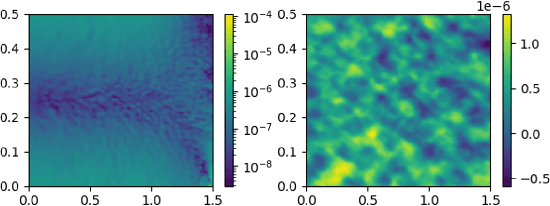

Recent advances in implicit neural representations show great promise when it comes to generating numerical solutions to partial differential equations (PDEs). Compared to conventional alternatives, such representations employ parameterized neural networks to define, in a mesh-free manner, signals that are highly-detailed, continuous, and fully differentiable. Most prior works aim to exploit these benefits in order to solve PDE-governed forward problems, or associated inverse problems that are defined by a small number of parameters. In this work, we present a novel machine learning approach to tackle topology optimization (TO) problems. Topology optimization refers to an important class of inverse problems that typically feature very high-dimensional parameter spaces and objective landscapes which are highly non-linear. To effectively leverage neural representations in the context of TO problems, we use multilayer perceptrons (MLPs) to parameterize both density and displacement fields. Using sensitivity analysis with a moving mean squared error, we show that our formulation can be used to efficiently minimize traditional structural compliance objectives. As we show through our experiments, a major benefit of our approach is that it enables self-supervised learning of continuous solution spaces to topology optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge