Not All LLM Reasoners Are Created Equal
Paper and Code
Oct 02, 2024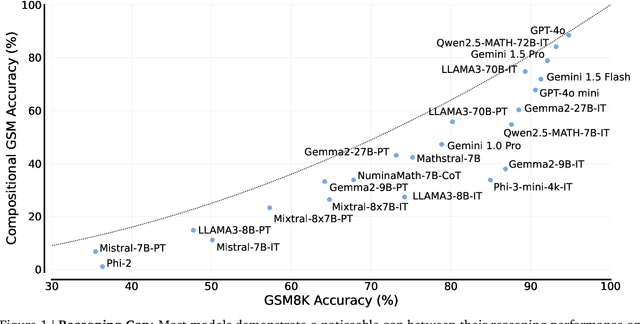
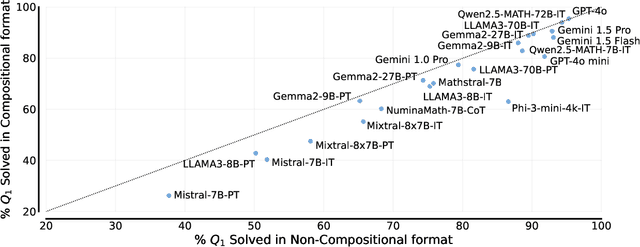
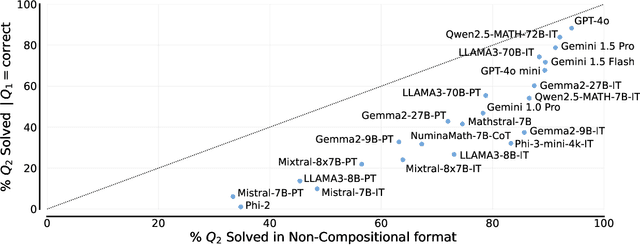
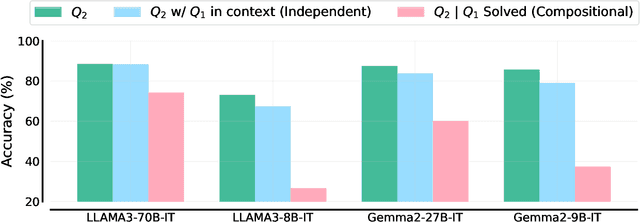
We study the depth of grade-school math (GSM) problem-solving capabilities of LLMs. To this end, we evaluate their performance on pairs of existing math word problems together so that the answer to the second problem depends on correctly answering the first problem. Our findings reveal a significant reasoning gap in most LLMs, that is performance difference between solving the compositional pairs and solving each question independently. This gap is more pronounced in smaller, more cost-efficient, and math-specialized models. Moreover, instruction-tuning recipes and code generation have varying effects across LLM sizes, while finetuning on GSM can lead to task overfitting. Our analysis indicates that large reasoning gaps are not because of test-set leakage, but due to distraction from additional context and poor second-hop reasoning. Overall, LLMs exhibit systematic differences in their reasoning abilities, despite what their performance on standard benchmarks indicates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge