Nonsmooth Composite Nonconvex-Concave Minimax Optimization

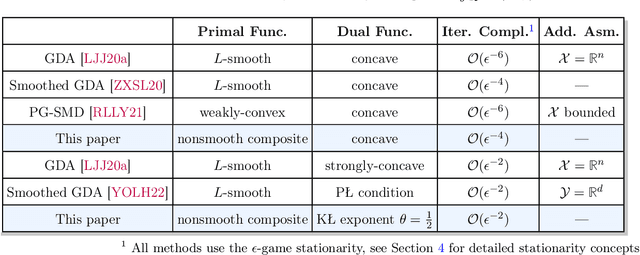
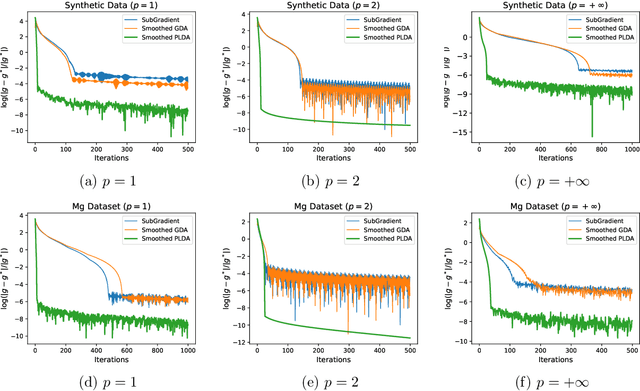
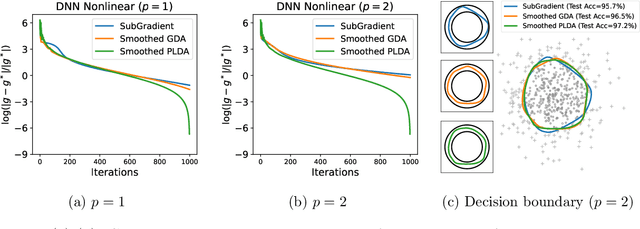
Nonconvex-concave minimax optimization has received intense interest in machine learning, including learning with robustness to data distribution, learning with non-decomposable loss, adversarial learning, to name a few. Nevertheless, most existing works focus on the gradient-descent-ascent (GDA) variants that can only be applied in smooth settings. In this paper, we consider a family of minimax problems whose objective function enjoys the nonsmooth composite structure in the variable of minimization and is concave in the variables of maximization. By fully exploiting the composite structure, we propose a smoothed proximal linear descent ascent (\textit{smoothed} PLDA) algorithm and further establish its $\mathcal{O}(\epsilon^{-4})$ iteration complexity, which matches that of smoothed GDA~\cite{zhang2020single} under smooth settings. Moreover, under the mild assumption that the objective function satisfies the one-sided Kurdyka-\L{}ojasiewicz condition with exponent $\theta \in (0,1)$, we can further improve the iteration complexity to $\mathcal{O}(\epsilon^{-2\max\{2\theta,1\}})$. To the best of our knowledge, this is the first provably efficient algorithm for nonsmooth nonconvex-concave problems that can achieve the optimal iteration complexity $\mathcal{O}(\epsilon^{-2})$ if $\theta \in (0,1/2]$. As a byproduct, we discuss different stationarity concepts and clarify their relationships quantitatively, which could be of independent interest. Empirically, we illustrate the effectiveness of the proposed smoothed PLDA in variation regularized Wasserstein distributionally robust optimization problems.