Nonparametric Spherical Topic Modeling with Word Embeddings
Paper and Code
Apr 01, 2016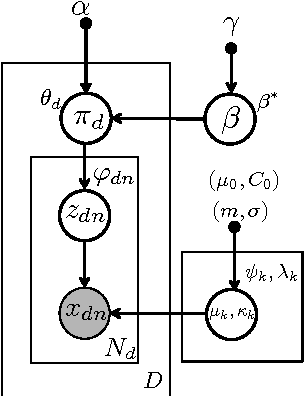
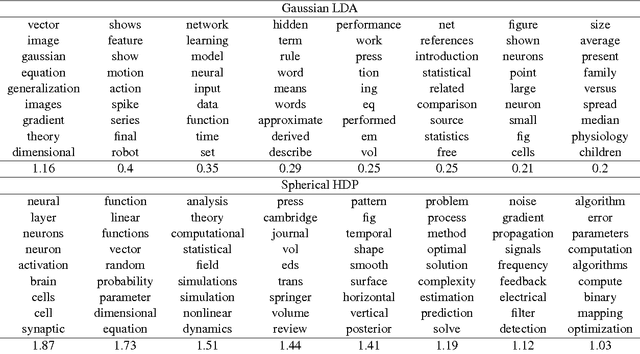

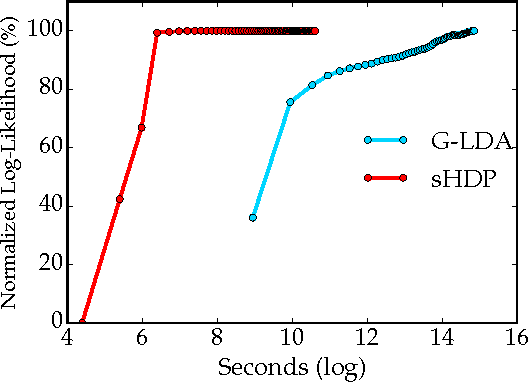
Traditional topic models do not account for semantic regularities in language. Recent distributional representations of words exhibit semantic consistency over directional metrics such as cosine similarity. However, neither categorical nor Gaussian observational distributions used in existing topic models are appropriate to leverage such correlations. In this paper, we propose to use the von Mises-Fisher distribution to model the density of words over a unit sphere. Such a representation is well-suited for directional data. We use a Hierarchical Dirichlet Process for our base topic model and propose an efficient inference algorithm based on Stochastic Variational Inference. This model enables us to naturally exploit the semantic structures of word embeddings while flexibly discovering the number of topics. Experiments demonstrate that our method outperforms competitive approaches in terms of topic coherence on two different text corpora while offering efficient inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge