Nonparametric Inference for Auto-Encoding Variational Bayes
Paper and Code
Dec 18, 2017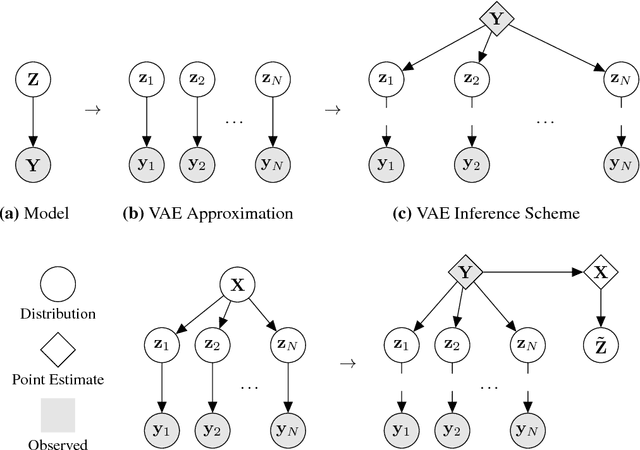
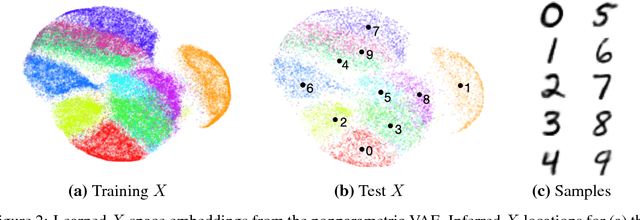
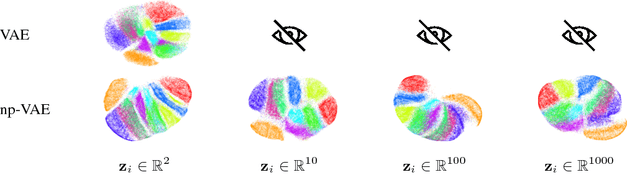

We would like to learn latent representations that are low-dimensional and highly interpretable. A model that has these characteristics is the Gaussian Process Latent Variable Model. The benefits and negative of the GP-LVM are complementary to the Variational Autoencoder, the former provides interpretable low-dimensional latent representations while the latter is able to handle large amounts of data and can use non-Gaussian likelihoods. Our inspiration for this paper is to marry these two approaches and reap the benefits of both. In order to do so we will introduce a novel approximate inference scheme inspired by the GP-LVM and the VAE. We show experimentally that the approximation allows the capacity of the generative bottle-neck (Z) of the VAE to be arbitrarily large without losing a highly interpretable representation, allowing reconstruction quality to be unlimited by Z at the same time as a low-dimensional space can be used to perform ancestral sampling from as well as a means to reason about the embedded data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge