Non-Convex Optimization with Certificates and Fast Rates Through Kernel Sums of Squares

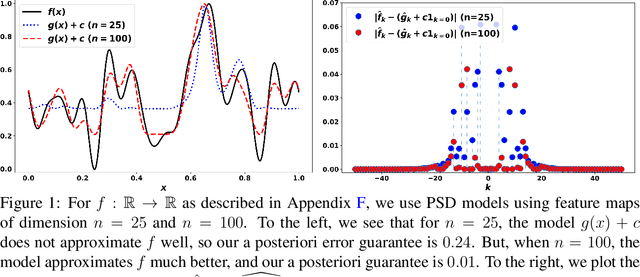
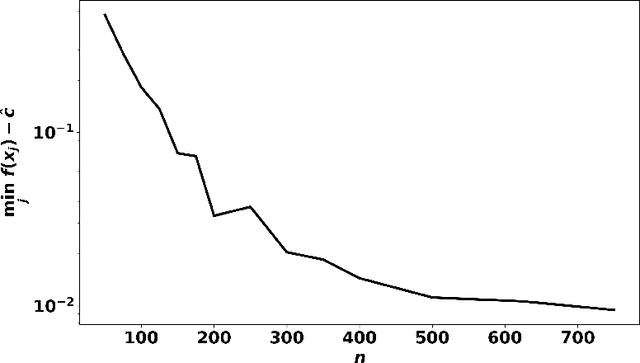
We consider potentially non-convex optimization problems, for which optimal rates of approximation depend on the dimension of the parameter space and the smoothness of the function to be optimized. In this paper, we propose an algorithm that achieves close to optimal a priori computational guarantees, while also providing a posteriori certificates of optimality. Our general formulation builds on infinite-dimensional sums-of-squares and Fourier analysis, and is instantiated on the minimization of multivariate periodic functions.