Noisy Adaptive Group Testing using Bayesian Sequential Experimental Design

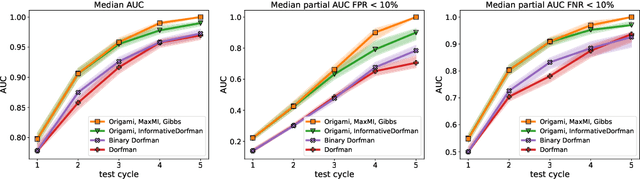
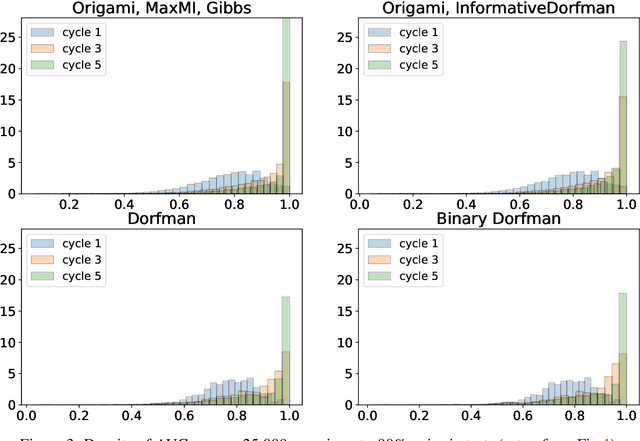
When test resources are scarce and infection prevalence is low, testing groups of individuals can be more efficient than testing individuals. This can be done by pooling individual samples (in groups, and only test those groups for the presence of a pathogen. The rationale is that if prevalence is low, many of these groups will ideally test negative, clearing all all individuals from such groups, whereas individuals appearing in (ideally few) positive groups will require further screening. Forming those groups in order to minimize testing costs while maintaining good detection is the goal of group testing algorithms. We propose a new framework to form such groups that takes into account various constraints of the testing environment, and which can easily incorporate individualized infection priors. Our solution solves a Bayesian sequential experimental design problem: Given previous group test results, we sample the posterior distribution of infection status vectors using sequential Monte Carlo samplers; these samples are then fed to an optimizer, which seeks to form groups that maximize an information gain if those future tests were to be known. To output marginal probabilities of infection, we use loopy belief propagation as a decoder. We show a significant empirical improvement over individualized tests in simulations: our G-MIMAX test procedure has an average specificity/sensitivity that significantly exceeds that of other baselines, including individual tests, as long as the disease prevalence $\leq 5\%$.