No Fuss Distance Metric Learning using Proxies
Paper and Code
Aug 01, 2017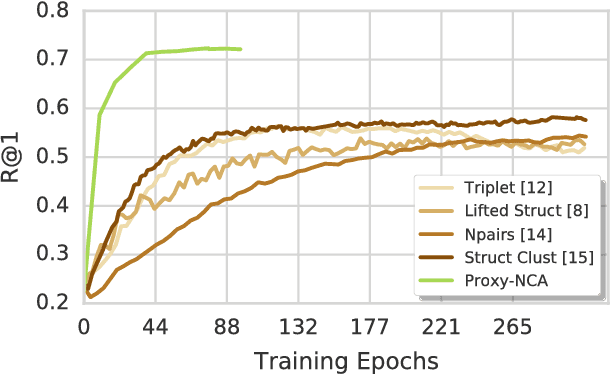
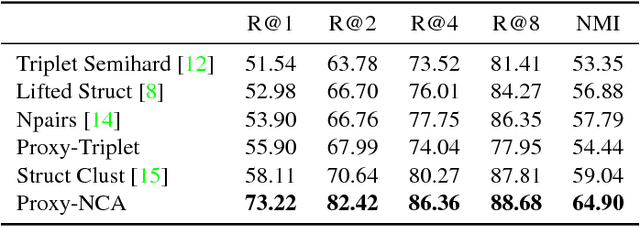
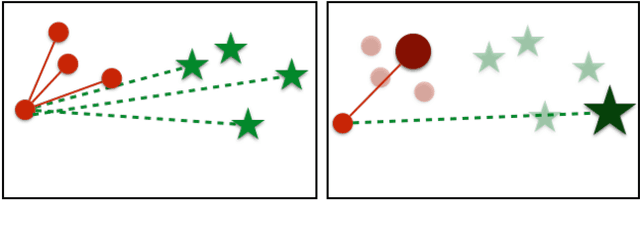
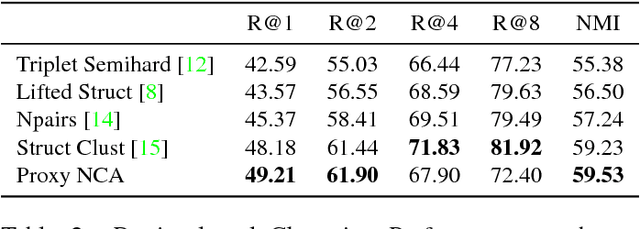
We address the problem of distance metric learning (DML), defined as learning a distance consistent with a notion of semantic similarity. Traditionally, for this problem supervision is expressed in the form of sets of points that follow an ordinal relationship -- an anchor point $x$ is similar to a set of positive points $Y$, and dissimilar to a set of negative points $Z$, and a loss defined over these distances is minimized. While the specifics of the optimization differ, in this work we collectively call this type of supervision Triplets and all methods that follow this pattern Triplet-Based methods. These methods are challenging to optimize. A main issue is the need for finding informative triplets, which is usually achieved by a variety of tricks such as increasing the batch size, hard or semi-hard triplet mining, etc. Even with these tricks, the convergence rate of such methods is slow. In this paper we propose to optimize the triplet loss on a different space of triplets, consisting of an anchor data point and similar and dissimilar proxy points which are learned as well. These proxies approximate the original data points, so that a triplet loss over the proxies is a tight upper bound of the original loss. This proxy-based loss is empirically better behaved. As a result, the proxy-loss improves on state-of-art results for three standard zero-shot learning datasets, by up to 15% points, while converging three times as fast as other triplet-based losses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge