New Oracle-Efficient Algorithms for Private Synthetic Data Release
Paper and Code
Jul 10, 2020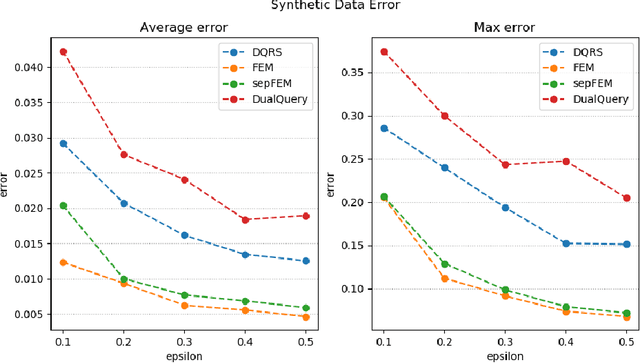
We present three new algorithms for constructing differentially private synthetic data---a sanitized version of a sensitive dataset that approximately preserves the answers to a large collection of statistical queries. All three algorithms are \emph{oracle-efficient} in the sense that they are computationally efficient when given access to an optimization oracle. Such an oracle can be implemented using many existing (non-private) optimization tools such as sophisticated integer program solvers. While the accuracy of the synthetic data is contingent on the oracle's optimization performance, the algorithms satisfy differential privacy even in the worst case. For all three algorithms, we provide theoretical guarantees for both accuracy and privacy. Through empirical evaluation, we demonstrate that our methods scale well with both the dimensionality of the data and the number of queries. Compared to the state-of-the-art method High-Dimensional Matrix Mechanism \cite{McKennaMHM18}, our algorithms provide better accuracy in the large workload and high privacy regime (corresponding to low privacy loss $\varepsilon$).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge