NeuroLGP-SM: A Surrogate-assisted Neuroevolution Approach using Linear Genetic Programming
Paper and Code
Mar 28, 2024
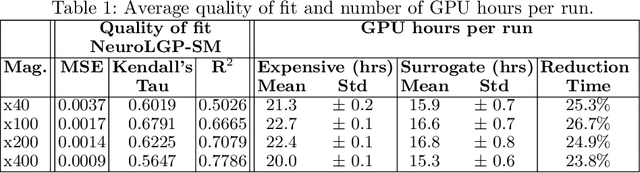
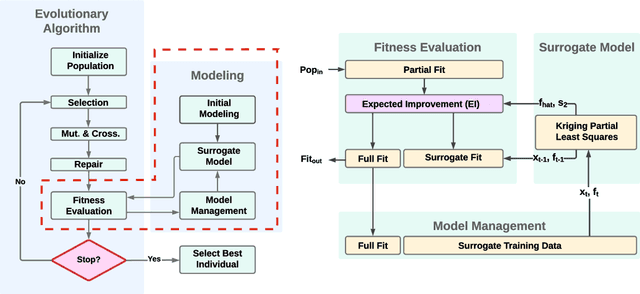
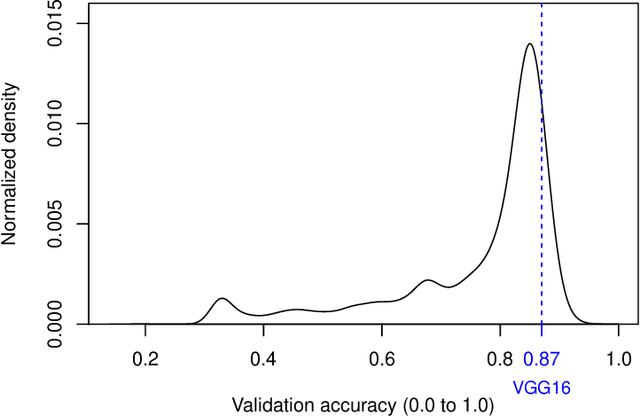
Evolutionary algorithms are increasingly recognised as a viable computational approach for the automated optimisation of deep neural networks (DNNs) within artificial intelligence. This method extends to the training of DNNs, an approach known as neuroevolution. However, neuroevolution is an inherently resource-intensive process, with certain studies reporting the consumption of thousands of GPU days for refining and training a single DNN network. To address the computational challenges associated with neuroevolution while still attaining good DNN accuracy, surrogate models emerge as a pragmatic solution. Despite their potential, the integration of surrogate models into neuroevolution is still in its early stages, hindered by factors such as the effective use of high-dimensional data and the representation employed in neuroevolution. In this context, we address these challenges by employing a suitable representation based on Linear Genetic Programming, denoted as NeuroLGP, and leveraging Kriging Partial Least Squares. The amalgamation of these two techniques culminates in our proposed methodology known as the NeuroLGP-Surrogate Model (NeuroLGP-SM). For comparison purposes, we also code and use a baseline approach incorporating a repair mechanism, a common practice in neuroevolution. Notably, the baseline approach surpasses the renowned VGG-16 model in accuracy. Given the computational intensity inherent in DNN operations, a singular run is typically the norm. To evaluate the efficacy of our proposed approach, we conducted 96 independent runs. Significantly, our methodologies consistently outperform the baseline, with the SM model demonstrating superior accuracy or comparable results to the NeuroLGP approach. Noteworthy is the additional advantage that the SM approach exhibits a 25% reduction in computational requirements, further emphasising its efficiency for neuroevolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge