Neural Vector Fields for Surface Representation and Inference

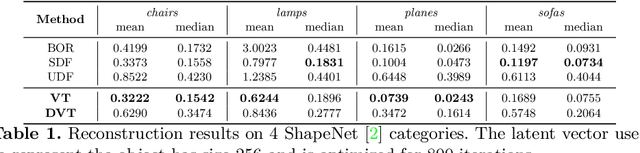
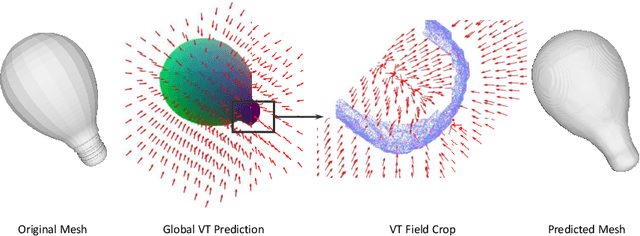
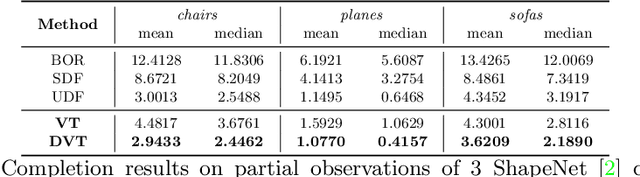
Neural implicit fields have recently been shown to represent 3D shapes accurately, opening up various applications in 3D shape analysis. Up to now, such implicit fields for 3D representation are scalar, encoding the signed distance or binary volume occupancy and more recently the unsigned distance. However, the first two can only represent closed shapes, while the unsigned distance has difficulties in accurate and fast shape inference. In this paper, we propose a Neural Vector Field for shape representation in order to overcome the two aforementioned problems. Mapping each point in space to the direction towards the closest surface, we can represent any type of shape. Similarly the shape mesh can be reconstructed by applying the marching cubes algorithm, with proposed small changes, on top of the inferred vector field. We compare the method on ShapeNet where the proposed new neural implicit field shows superior accuracy in representing both closed and open shapes outperforming previous methods.