Neural Surface Maps
Paper and Code
Mar 31, 2021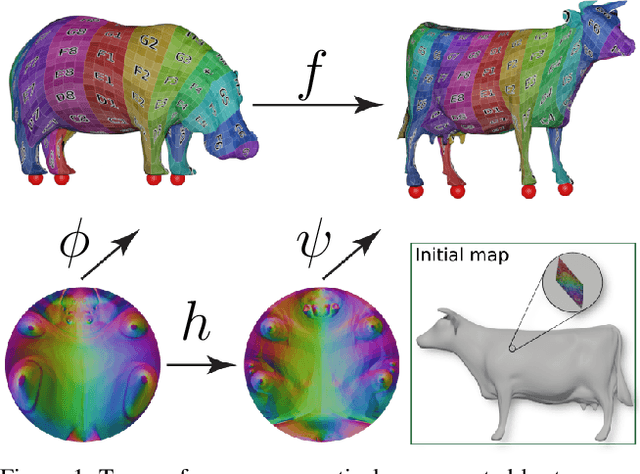

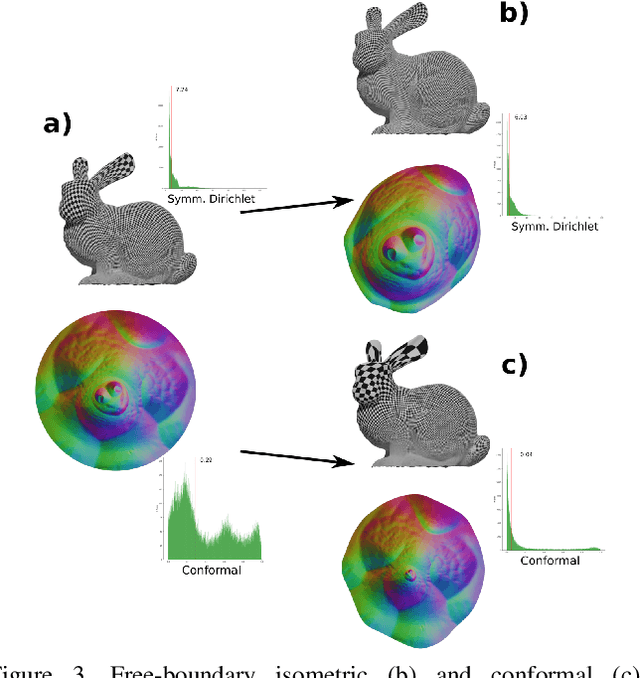

Maps are arguably one of the most fundamental concepts used to define and operate on manifold surfaces in differentiable geometry. Accordingly, in geometry processing, maps are ubiquitous and are used in many core applications, such as paramterization, shape analysis, remeshing, and deformation. Unfortunately, most computational representations of surface maps do not lend themselves to manipulation and optimization, usually entailing hard, discrete problems. While algorithms exist to solve these problems, they are problem-specific, and a general framework for surface maps is still in need. In this paper, we advocate considering neural networks as encoding surface maps. Since neural networks can be composed on one another and are differentiable, we show it is easy to use them to define surfaces via atlases, compose them for surface-to-surface mappings, and optimize differentiable objectives relating to them, such as any notion of distortion, in a trivial manner. In our experiments, we represent surfaces by generating a neural map that approximates a UV parameterization of a 3D model. Then, we compose this map with other neural maps which we optimize with respect to distortion measures. We show that our formulation enables trivial optimization of rather elusive mapping tasks, such as maps between a collection of surfaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge