Neural-Guided Symbolic Regression with Semantic Prior

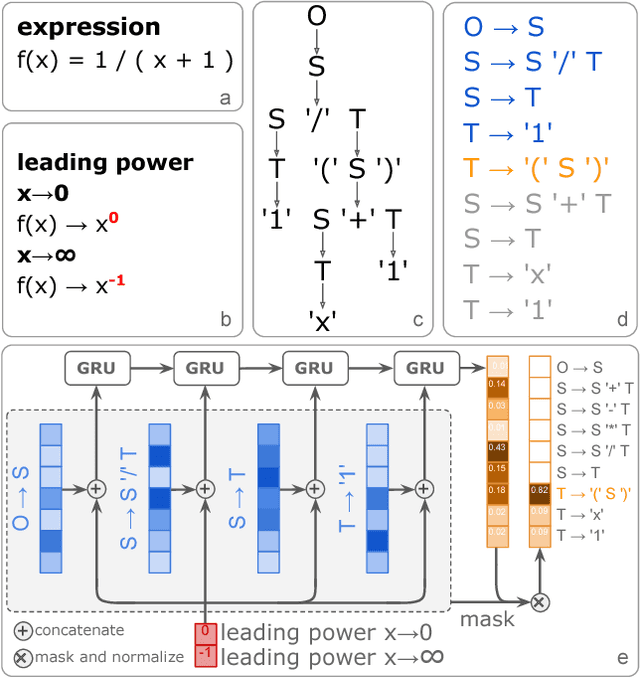
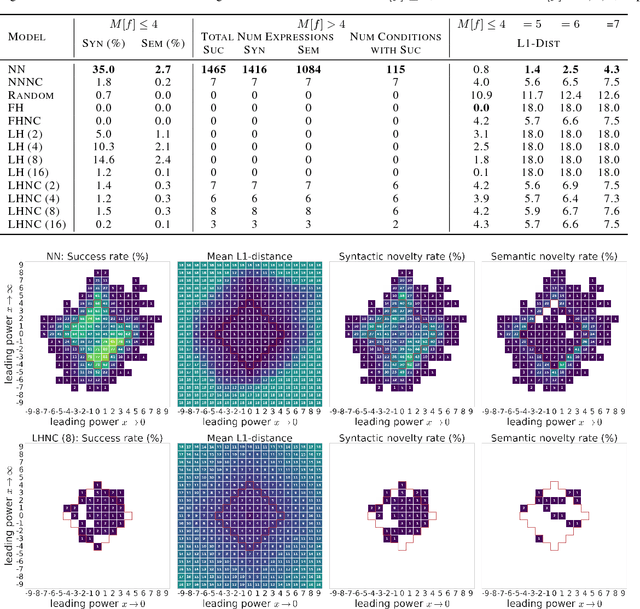
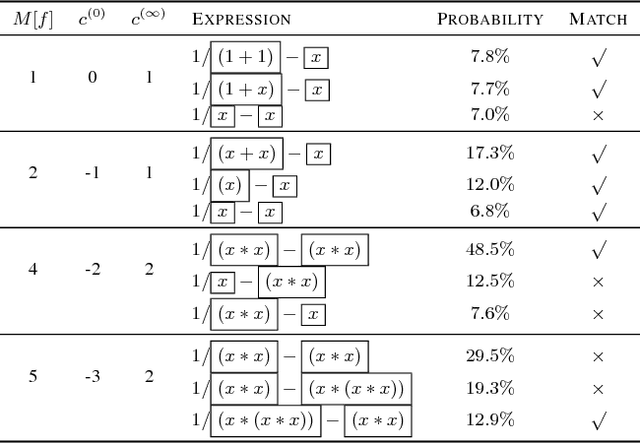
Symbolic regression has been shown to be quite useful in many domains from discovering scientific laws to industrial empirical modeling. Existing methods focus on numerically fitting the given data. However, in many domains, symbolically derivable properties of the desired expressions are known. We illustrate these "semantic priors" with leading powers (the polynomial behavior as the input approaches 0 and $\infty$). We introduce an expression generating neural network that significantly favors the generation of expressions with desired leading powers, even generalizing to powers not in the training set. We then describe our Neural-Guided Monte Carlo Tree Search (NG-MCTS) algorithm for symbolic regression. We extensively evaluate our method on thousands of symbolic regression tasks and desired expressions to show that it significantly outperforms baseline algorithms and exhibits discovery of novel expressions outside of the training set.