Neural Embeddings of Graphs in Hyperbolic Space
Paper and Code
May 29, 2017
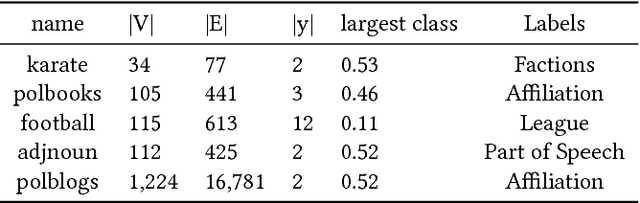
Neural embeddings have been used with great success in Natural Language Processing (NLP). They provide compact representations that encapsulate word similarity and attain state-of-the-art performance in a range of linguistic tasks. The success of neural embeddings has prompted significant amounts of research into applications in domains other than language. One such domain is graph-structured data, where embeddings of vertices can be learned that encapsulate vertex similarity and improve performance on tasks including edge prediction and vertex labelling. For both NLP and graph based tasks, embeddings have been learned in high-dimensional Euclidean spaces. However, recent work has shown that the appropriate isometric space for embedding complex networks is not the flat Euclidean space, but negatively curved, hyperbolic space. We present a new concept that exploits these recent insights and propose learning neural embeddings of graphs in hyperbolic space. We provide experimental evidence that embedding graphs in their natural geometry significantly improves performance on downstream tasks for several real-world public datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge