Neural Architecture Search using Bayesian Optimisation with Weisfeiler-Lehman Kernel

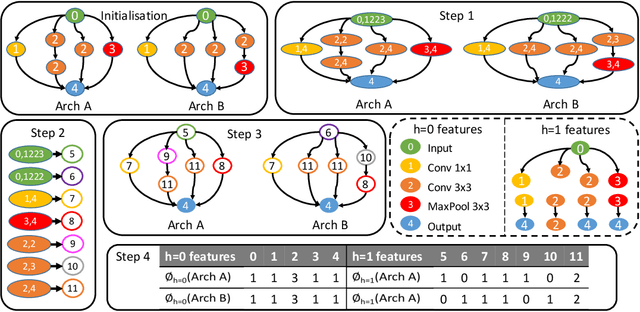
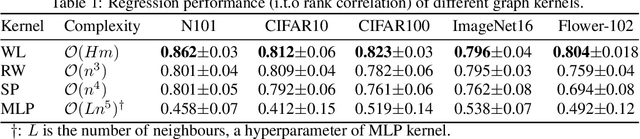
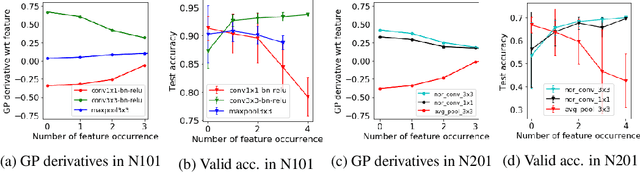
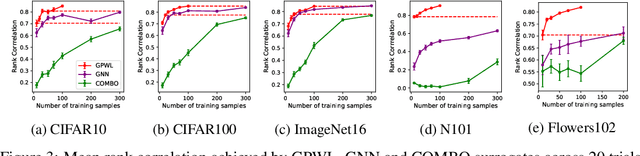
Bayesian optimisation (BO) has been widely used for hyperparameter optimisation but its application in neural architecture search (NAS) is limited due to the non-continuous, high-dimensional and graph-like search spaces. Current approaches either rely on encoding schemes, which are not scalable to large architectures and ignore the implicit topological structure of architectures, or use graph neural networks, which require additional hyperparameter tuning and a large amount of observed data, which is particularly expensive to obtain in NAS. We propose a neat BO approach for NAS, which combines the Weisfeiler-Lehman graph kernel with a Gaussian process surrogate to capture the topological structure of architectures, without having to explicitly define a Gaussian process over high-dimensional vector spaces. We also harness the interpretable features learnt via the graph kernel to guide the generation of new architectures. We demonstrate empirically that our surrogate model is scalable to large architectures and highly data-efficient; competing methods require 3 to 20 times more observations to achieve equally good prediction performance as ours. We finally show that our method outperforms existing NAS approaches to achieve state-of-the-art results on NAS datasets.