Neighborhood Gradient Clustering: An Efficient Decentralized Learning Method for Non-IID Data Distributions
Paper and Code
Sep 30, 2022
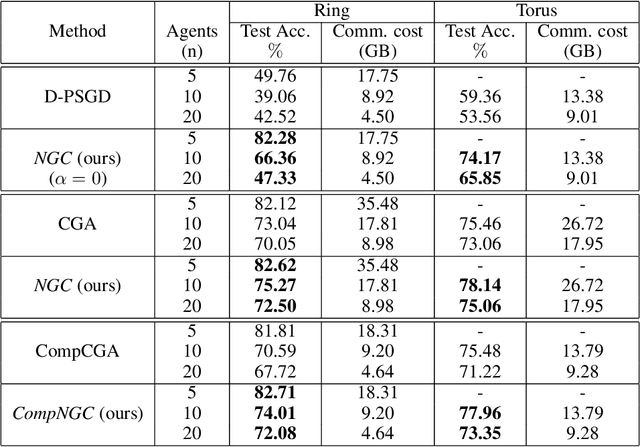

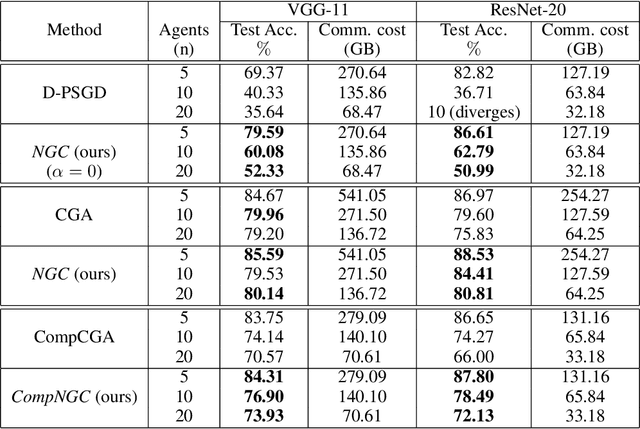
Decentralized learning algorithms enable the training of deep learning models over large distributed datasets generated at different devices and locations, without the need for a central server. In practical scenarios, the distributed datasets can have significantly different data distributions across the agents. The current state-of-the-art decentralized algorithms mostly assume the data distributions to be Independent and Identically Distributed (IID). This paper focuses on improving decentralized learning over non-IID data distributions with minimal compute and memory overheads. We propose Neighborhood Gradient Clustering (NGC), a novel decentralized learning algorithm that modifies the local gradients of each agent using self- and cross-gradient information. In particular, the proposed method replaces the local gradients of the model with the weighted mean of the self-gradients, model-variant cross-gradients (derivatives of the received neighbors' model parameters with respect to the local dataset), and data-variant cross-gradients (derivatives of the local model with respect to its neighbors' datasets). Further, we present CompNGC, a compressed version of NGC that reduces the communication overhead by $32 \times$ by compressing the cross-gradients. We demonstrate the empirical convergence and efficiency of the proposed technique over non-IID data distributions sampled from the CIFAR-10 dataset on various model architectures and graph topologies. Our experiments demonstrate that NGC and CompNGC outperform the existing state-of-the-art (SoTA) decentralized learning algorithm over non-IID data by $1-5\%$ with significantly less compute and memory requirements. Further, we also show that the proposed NGC method outperforms the baseline by $5-40\%$ with no additional communication.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge