NECST: Neural Joint Source-Channel Coding
Paper and Code
Nov 19, 2018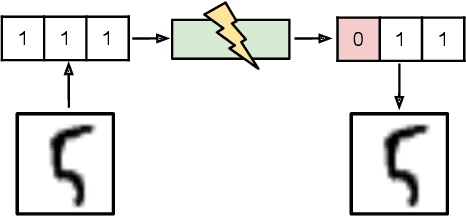

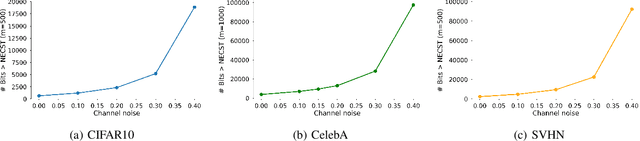
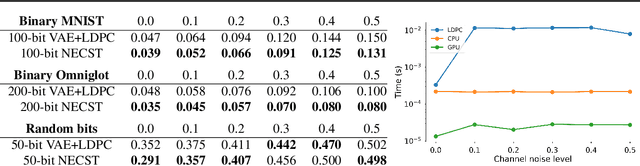
For reliable transmission across a noisy communication channel, classical results from information theory show that it is asymptotically optimal to separate out the source and channel coding processes. However, this decomposition can fall short in the finite bit-length regime, as it requires non-trivial tuning of hand-crafted codes and assumes infinite computational power for decoding. In this work, we propose Neural Error Correcting and Source Trimming (\modelname) codes to jointly learn the encoding and decoding processes in an end-to-end fashion. By adding noise into the latent codes to simulate the channel during training, we learn to both compress and error-correct given a fixed bit-length and computational budget. We obtain codes that are not only competitive against several capacity-approaching channel codes, but also learn useful robust representations of the data for downstream tasks such as classification. Finally, we learn an extremely fast neural decoder, yielding almost an order of magnitude in speedup compared to standard decoding methods based on iterative belief propagation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge