NDDEs: A Deep Neural Network Framework for Solving Forward and Inverse Problems in Delay Differential Equations
Paper and Code
Aug 17, 2024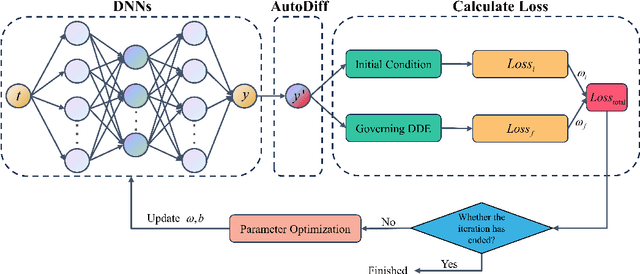

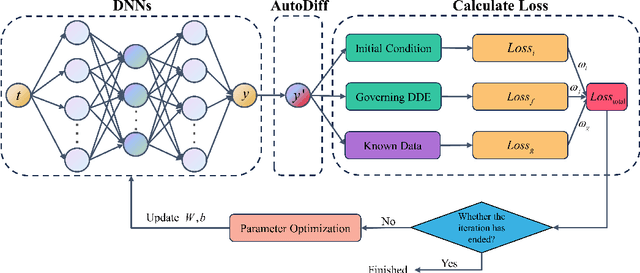

This article proposes a solution framework for delay differential equations (DDEs) based on deep neural networks (DNNs) - the neural delay differential equations (NDDEs), aimed at solving the forward and inverse problems of delay differential equations. This framework embeds the delay differential equations into the neural networks to accommodate the diverse requirements of DDEs in terms of initial conditions, control equations, and known data. NDDEs adjust the network parameters through automatic differentiation and optimization algorithms to minimize the loss function, thereby obtaining numerical solutions to the delay differential equations without the grid dependence and discretization errors typical of traditional numerical methods. In addressing inverse problems, the NDDE framework can utilize observational data to perform precise estimation of single or multiple delay parameters. The results of multiple numerical experiments have shown that NDDEs demonstrate high precision in both forward and inverse problems, proving their effectiveness and promising potential in dealing with delayed differential equation issues.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge