Naïve regression requires weaker assumptions than factor models to adjust for multiple cause confounding
Paper and Code
Jul 24, 2020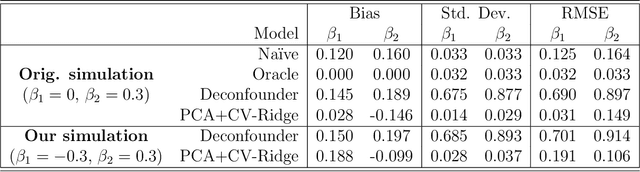
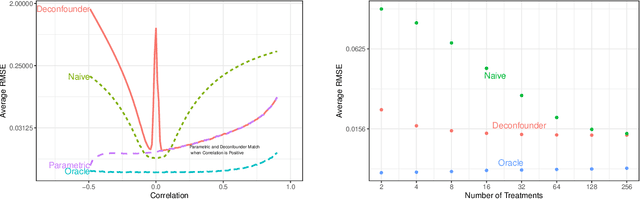
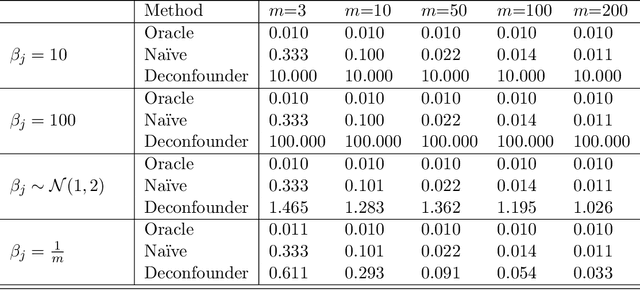

The empirical practice of using factor models to adjust for shared, unobserved confounders, $\mathbf{Z}$, in observational settings with multiple treatments, $\mathbf{A}$, is widespread in fields including genetics, networks, medicine, and politics. Wang and Blei (2019, WB) formalizes these procedures and develops the "deconfounder," a causal inference method using factor models of $\mathbf{A}$ to estimate "substitute confounders," $\hat{\mathbf{Z}}$, then estimating treatment effects by regressing the outcome, $\mathbf{Y}$, on part of $\mathbf{A}$ while adjusting for $\hat{\mathbf{Z}}$. WB claim the deconfounder is unbiased when there are no single-cause confounders and $\hat{\mathbf{Z}}$ is "pinpointed." We clarify pinpointing requires each confounder to affect infinitely many treatments. We prove under these assumptions, a na\"ive semiparametric regression of $\mathbf{Y}$ on $\mathbf{A}$ is asymptotically unbiased. Deconfounder variants nesting this regression are therefore also asymptotically unbiased, but variants using $\hat{\mathbf{Z}}$ and subsets of causes require further untestable assumptions. We replicate every deconfounder analysis with available data and find it fails to consistently outperform na\"ive regression. In practice, the deconfounder produces implausible estimates in WB's case study to movie earnings: estimates suggest comic author Stan Lee's cameo appearances causally contributed \$15.5 billion, most of Marvel movie revenue. We conclude neither approach is a viable substitute for careful research design in real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge