Multitask Online Mirror Descent
Paper and Code
Jun 04, 2021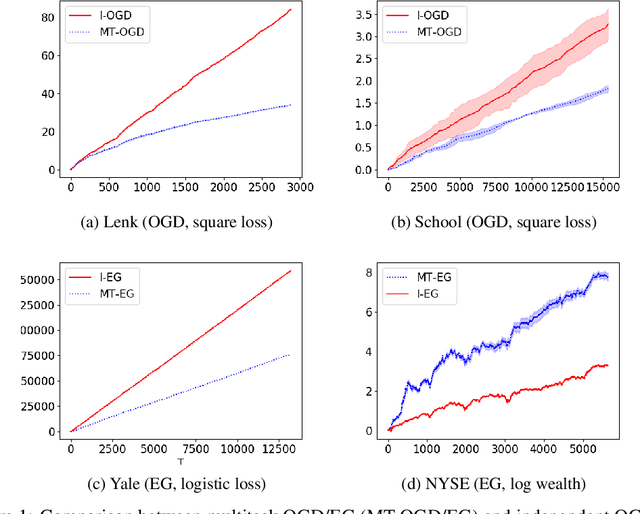

We introduce and analyze MT-OMD, a multitask generalization of Online Mirror Descent (OMD) which operates by sharing updates between tasks. We prove that the regret of MT-OMD is of order $\sqrt{1 + \sigma^2(N-1)}\sqrt{T}$, where $\sigma^2$ is the task variance according to the geometry induced by the regularizer, $N$ is the number of tasks, and $T$ is the time horizon. Whenever tasks are similar, that is, $\sigma^2 \le 1$, this improves upon the $\sqrt{NT}$ bound obtained by running independent OMDs on each task. Our multitask extensions of Online Gradient Descent and Exponentiated Gradient, two important instances of OMD, are shown to enjoy closed-form updates, making them easy to use in practice. Finally, we provide numerical experiments on four real-world datasets which support our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge