Multiple Kernel Clustering with Dual Noise Minimization
Paper and Code
Jul 13, 2022

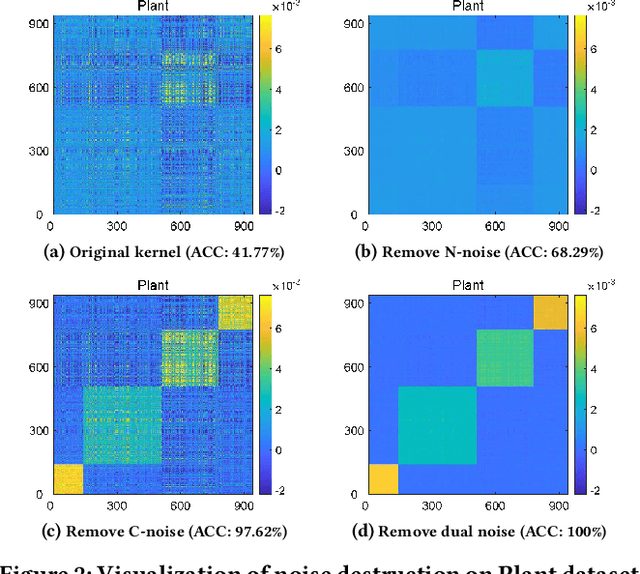
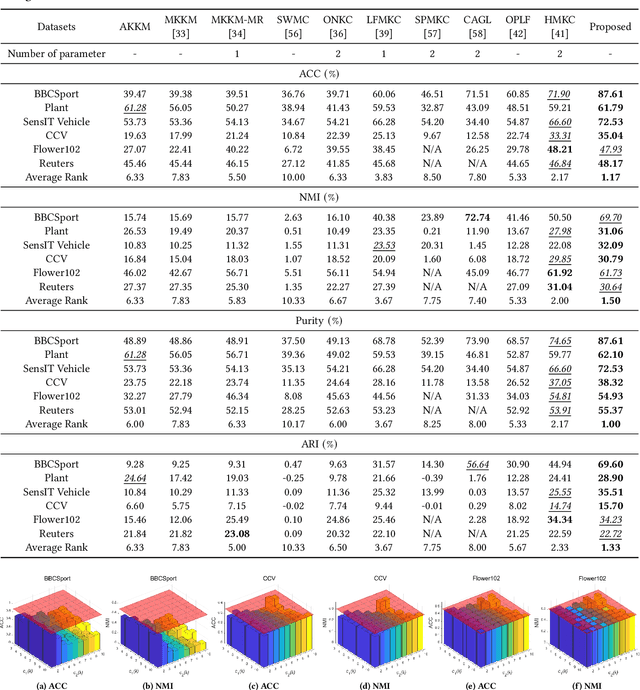
Clustering is a representative unsupervised method widely applied in multi-modal and multi-view scenarios. Multiple kernel clustering (MKC) aims to group data by integrating complementary information from base kernels. As a representative, late fusion MKC first decomposes the kernels into orthogonal partition matrices, then learns a consensus one from them, achieving promising performance recently. However, these methods fail to consider the noise inside the partition matrix, preventing further improvement of clustering performance. We discover that the noise can be disassembled into separable dual parts, i.e. N-noise and C-noise (Null space noise and Column space noise). In this paper, we rigorously define dual noise and propose a novel parameter-free MKC algorithm by minimizing them. To solve the resultant optimization problem, we design an efficient two-step iterative strategy. To our best knowledge, it is the first time to investigate dual noise within the partition in the kernel space. We observe that dual noise will pollute the block diagonal structures and incur the degeneration of clustering performance, and C-noise exhibits stronger destruction than N-noise. Owing to our efficient mechanism to minimize dual noise, the proposed algorithm surpasses the recent methods by large margins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge