Multiple Greedy Quasi-Newton Methods for Saddle Point Problems
Paper and Code
Aug 01, 2024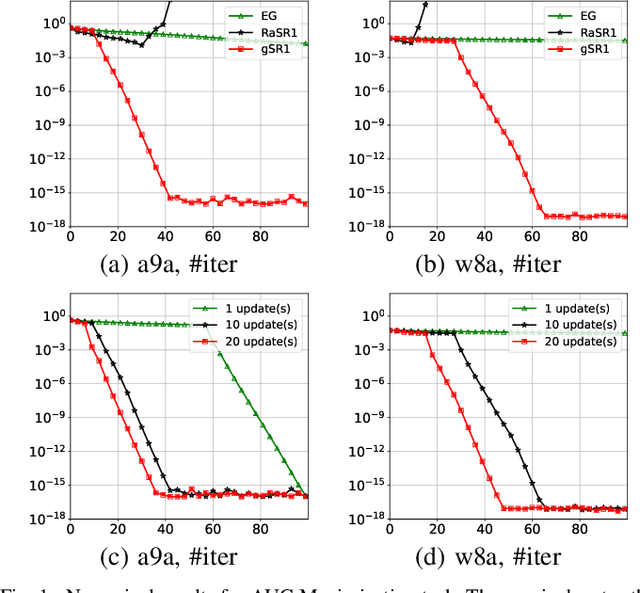
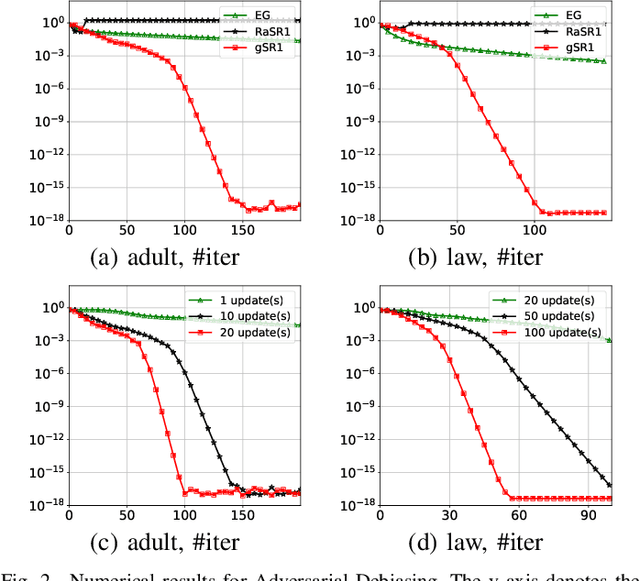
This paper introduces the Multiple Greedy Quasi-Newton (MGSR1-SP) method, a novel approach to solving strongly-convex-strongly-concave (SCSC) saddle point problems. Our method enhances the approximation of the squared indefinite Hessian matrix inherent in these problems, significantly improving both stability and efficiency through iterative greedy updates. We provide a thorough theoretical analysis of MGSR1-SP, demonstrating its linear-quadratic convergence rate. Numerical experiments conducted on AUC maximization and adversarial debiasing problems, compared with state-of-the-art algorithms, underscore our method's enhanced convergence rate. These results affirm the potential of MGSR1-SP to improve performance across a broad spectrum of machine learning applications where efficient and accurate Hessian approximations are crucial.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge