Multilevel Gibbs Sampling for Bayesian Regression
Paper and Code
Sep 25, 2020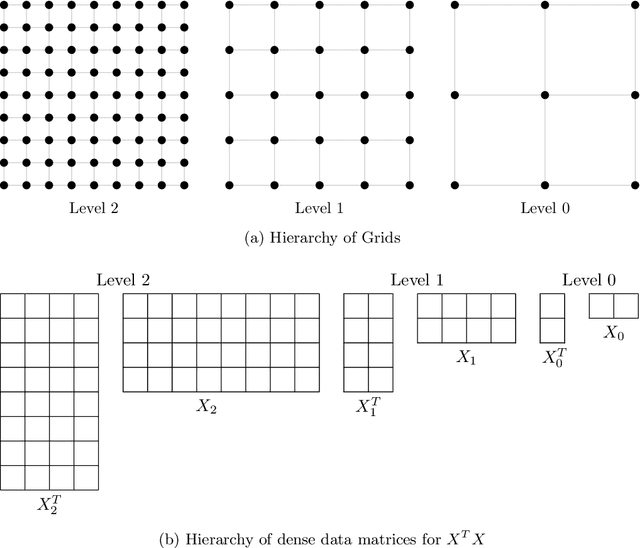



Bayesian regression remains a simple but effective tool based on Bayesian inference techniques. For large-scale applications, with complicated posterior distributions, Markov Chain Monte Carlo methods are applied. To improve the well-known computational burden of Markov Chain Monte Carlo approach for Bayesian regression, we developed a multilevel Gibbs sampler for Bayesian regression of linear mixed models. The level hierarchy of data matrices is created by clustering the features and/or samples of data matrices. Additionally, the use of correlated samples is investigated for variance reduction to improve the convergence of the Markov Chain. Testing on a diverse set of data sets, speed-up is achieved for almost all of them without significant loss in predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge