Multidimensional Membership Mixture Models
Paper and Code
Aug 02, 2012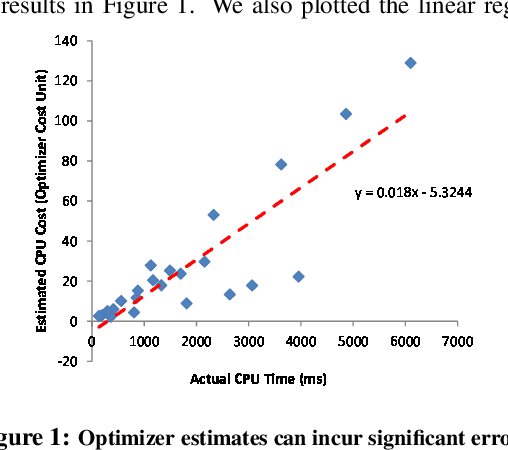

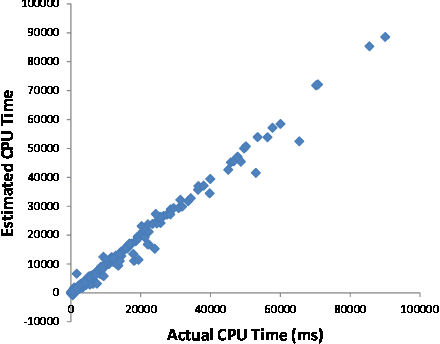
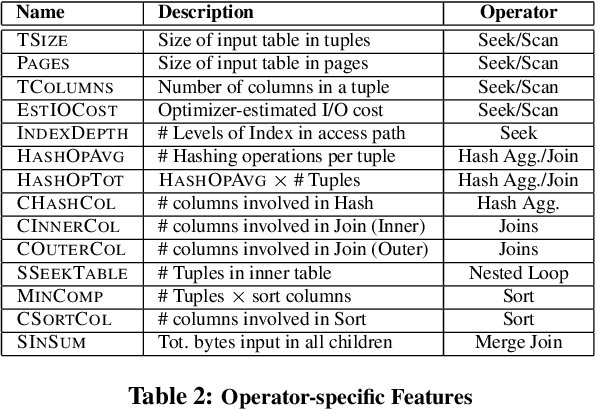
We present the multidimensional membership mixture (M3) models where every dimension of the membership represents an independent mixture model and each data point is generated from the selected mixture components jointly. This is helpful when the data has a certain shared structure. For example, three unique means and three unique variances can effectively form a Gaussian mixture model with nine components, while requiring only six parameters to fully describe it. In this paper, we present three instantiations of M3 models (together with the learning and inference algorithms): infinite, finite, and hybrid, depending on whether the number of mixtures is fixed or not. They are built upon Dirichlet process mixture models, latent Dirichlet allocation, and a combination respectively. We then consider two applications: topic modeling and learning 3D object arrangements. Our experiments show that our M3 models achieve better performance using fewer topics than many classic topic models. We also observe that topics from the different dimensions of M3 models are meaningful and orthogonal to each other.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge