Multichannel Compressive Sensing MRI Using Noiselet Encoding
Paper and Code
Jul 22, 2014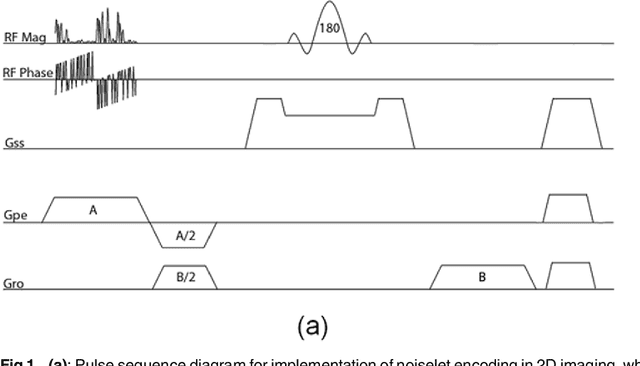
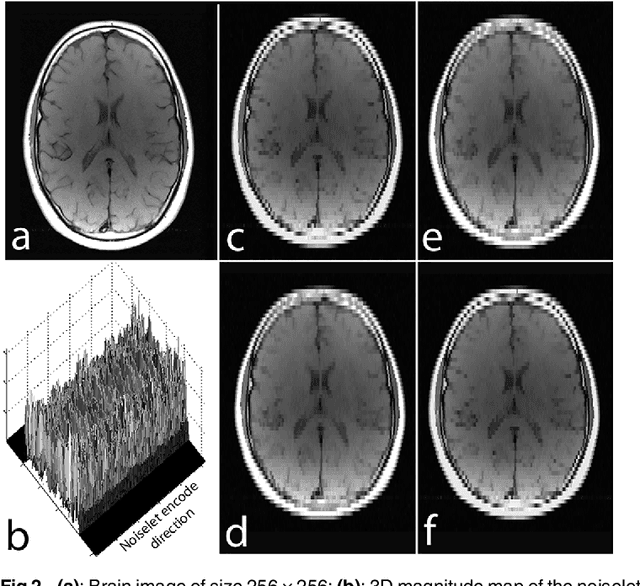
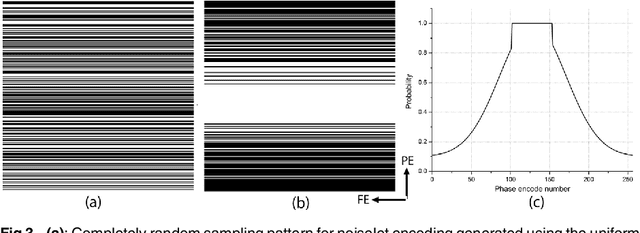
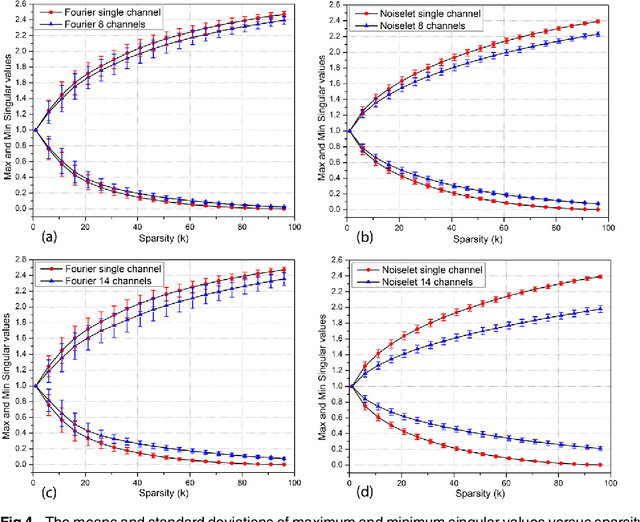
The incoherence between measurement and sparsifying transform matrices and the restricted isometry property (RIP) of measurement matrix are two of the key factors in determining the performance of compressive sensing (CS). In CS-MRI, the randomly under-sampled Fourier matrix is used as the measurement matrix and the wavelet transform is usually used as sparsifying transform matrix. However, the incoherence between the randomly under-sampled Fourier matrix and the wavelet matrix is not optimal, which can deteriorate the performance of CS-MRI. Using the mathematical result that noiselets are maximally incoherent with wavelets, this paper introduces the noiselet unitary bases as the measurement matrix to improve the incoherence and RIP in CS-MRI, and presents a method to design the pulse sequence for the noiselet encoding. This novel encoding scheme is combined with the multichannel compressive sensing (MCS) framework to take the advantage of multichannel data acquisition used in MRI scanners. An empirical RIP analysis is presented to compare the multichannel noiselet and multichannel Fourier measurement matrices in MCS. Simulations are presented in the MCS framework to compare the performance of noiselet encoding reconstructions and Fourier encoding reconstructions at different acceleration factors. The comparisons indicate that multichannel noiselet measurement matrix has better RIP than that of its Fourier counterpart, and that noiselet encoded MCS-MRI outperforms Fourier encoded MCS-MRI in preserving image resolution and can achieve higher acceleration factors. To demonstrate the feasibility of the proposed noiselet encoding scheme, two pulse sequences with tailored spatially selective RF excitation pulses was designed and implemented on a 3T scanner to acquire the data in the noiselet domain from a phantom and a human brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge