Multi Type Mean Field Reinforcement Learning
Paper and Code
Mar 09, 2020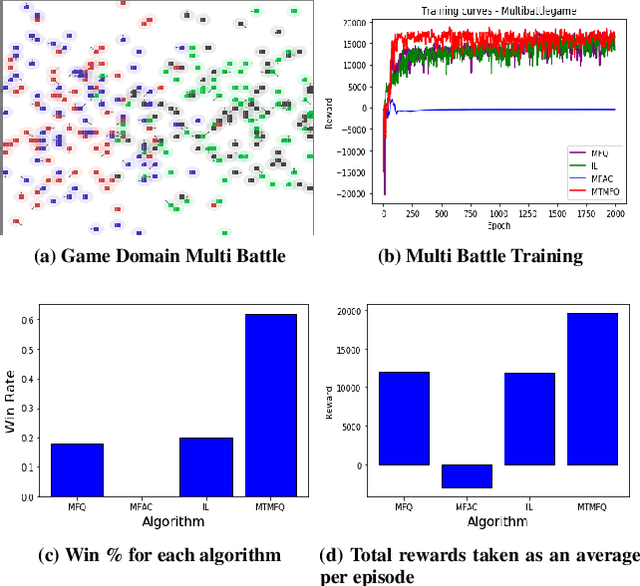
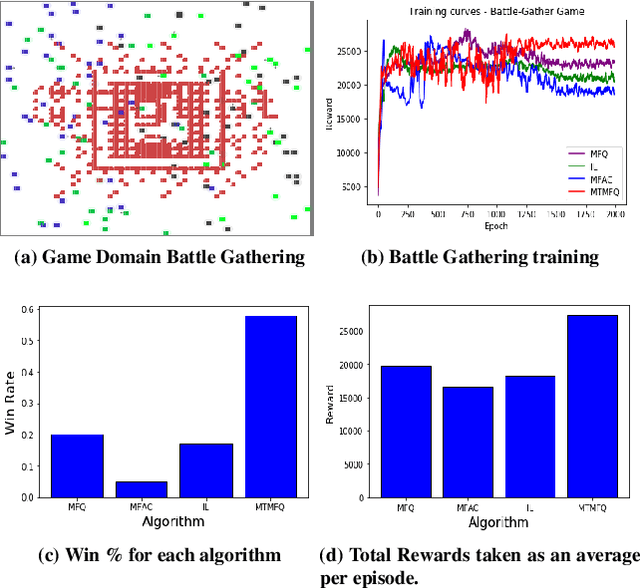
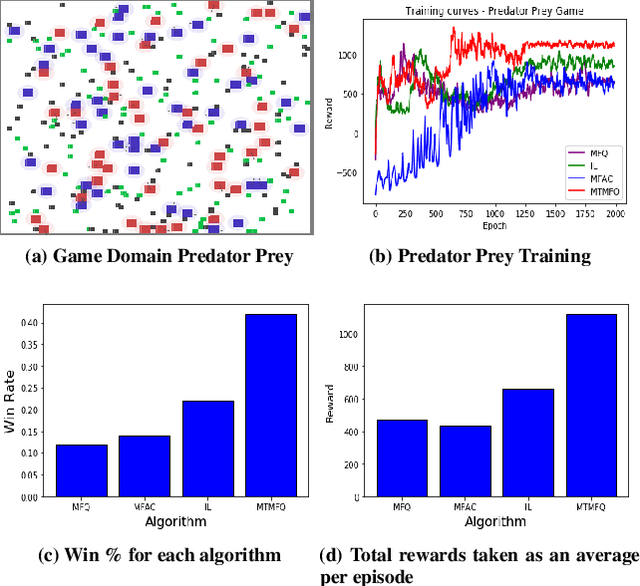
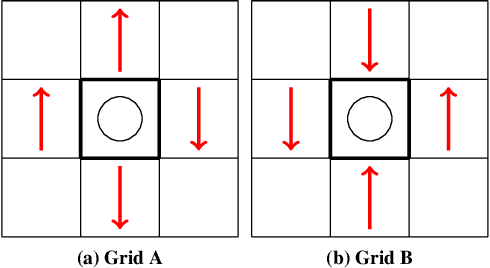
Mean field theory provides an effective way of scaling multiagent reinforcement learning algorithms to environments with many agents that can be abstracted by a virtual mean agent. In this paper, we extend mean field multiagent algorithms to multiple types. The types enable the relaxation of a core assumption in mean field games, which is that all agents in the environment are playing almost similar strategies and have the same goal. We conduct experiments on three different testbeds for the field of many agent reinforcement learning, based on the standard MAgents framework. We consider two different kinds of mean field games: a) Games where agents belong to predefined types that are known a priori and b) Games where the type of each agent is unknown and therefore must be learned based on observations. We introduce new algorithms for each type of game and demonstrate their superior performance over state of the art algorithms that assume that all agents belong to the same type and other baseline algorithms in the MAgent framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge