Multi-Source Causal Inference Using Control Variates

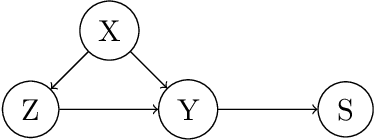
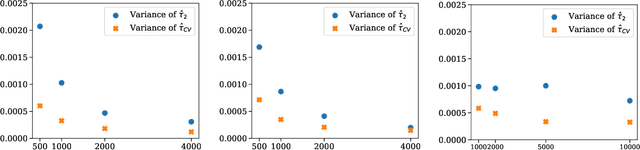
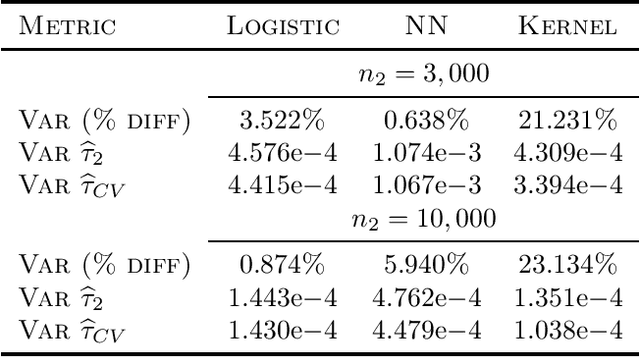
While many areas of machine learning have benefited from the increasing availability of large and varied datasets, the benefit to causal inference has been limited given the strong assumptions needed to ensure identifiability of causal effects; these are often not satisfied in real-world datasets. For example, many large observational datasets (e.g., case-control studies in epidemiology, click-through data in recommender systems) suffer from selection bias on the outcome, which makes the average treatment effect (ATE) unidentifiable. We propose a general algorithm to estimate causal effects from \emph{multiple} data sources, where the ATE may be identifiable only in some datasets but not others. The key idea is to construct control variates using the datasets in which the ATE is not identifiable. We show theoretically that this reduces the variance of the ATE estimate. We apply this framework to inference from observational data under an outcome selection bias, assuming access to an auxiliary small dataset from which we can obtain a consistent estimate of the ATE. We construct a control variate by taking the difference of the odds ratio estimates from the two datasets. Across simulations and two case studies with real data, we show that this control variate can significantly reduce the variance of the ATE estimate.