Multi-Objective Policy Gradients with Topological Constraints
Paper and Code
Sep 15, 2022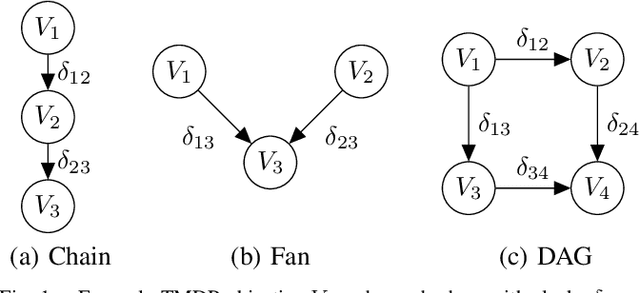


Multi-objective optimization models that encode ordered sequential constraints provide a solution to model various challenging problems including encoding preferences, modeling a curriculum, and enforcing measures of safety. A recently developed theory of topological Markov decision processes (TMDPs) captures this range of problems for the case of discrete states and actions. In this work, we extend TMDPs towards continuous spaces and unknown transition dynamics by formulating, proving, and implementing the policy gradient theorem for TMDPs. This theoretical result enables the creation of TMDP learning algorithms that use function approximators, and can generalize existing deep reinforcement learning (DRL) approaches. Specifically, we present a new algorithm for a policy gradient in TMDPs by a simple extension of the proximal policy optimization (PPO) algorithm. We demonstrate this on a real-world multiple-objective navigation problem with an arbitrary ordering of objectives both in simulation and on a real robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge