Multi-kernel Correntropy-based Orientation Estimation of IMUs: Gradient Descent Methods
Paper and Code
Apr 13, 2023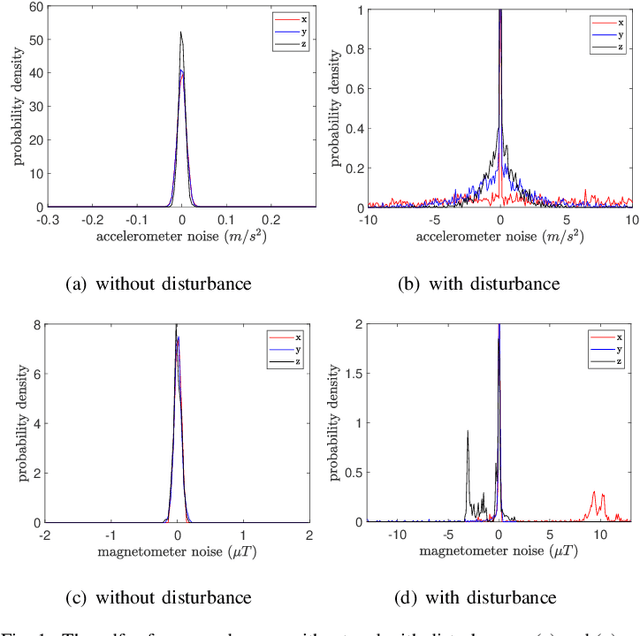
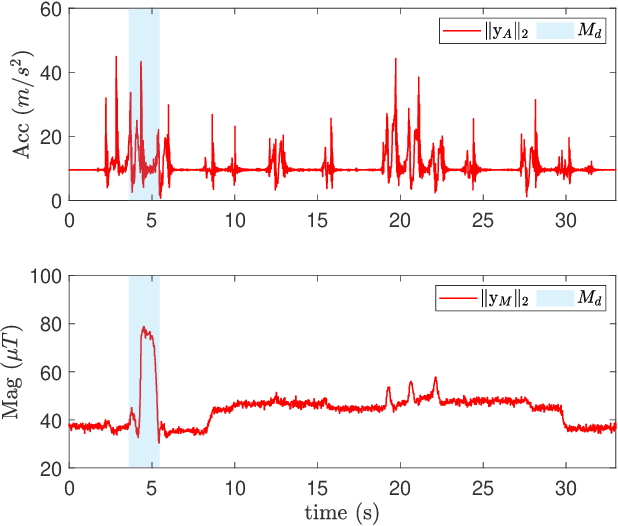
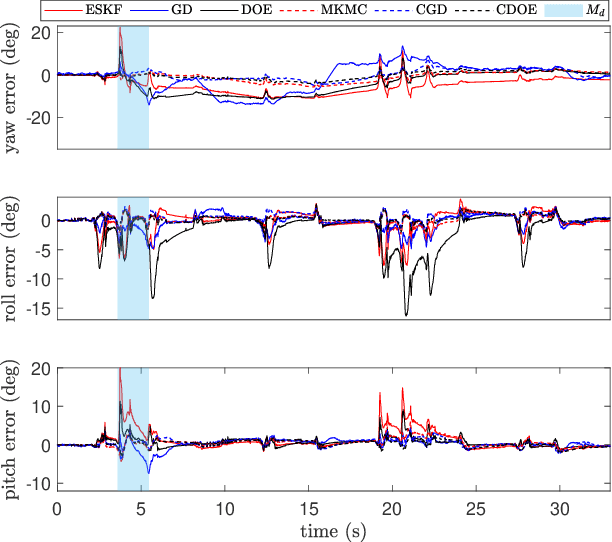
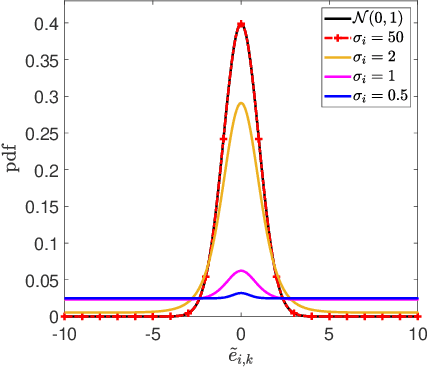
This paper presents two computationally efficient algorithms for the orientation estimation of inertial measurement units (IMUs): the correntropy-based gradient descent (CGD) and the correntropy-based decoupled orientation estimation (CDOE). Traditional methods, such as gradient descent (GD) and decoupled orientation estimation (DOE), rely on the mean squared error (MSE) criterion, making them vulnerable to external acceleration and magnetic interference. To address this issue, we demonstrate that the multi-kernel correntropy loss (MKCL) is an optimal objective function for maximum likelihood estimation (MLE) when the noise follows a type of heavy-tailed distribution. In certain situations, the estimation error of the MKCL is bounded even in the presence of arbitrarily large outliers. By replacing the standard MSE cost function with MKCL, we develop the CGD and CDOE algorithms. We evaluate the effectiveness of our proposed methods by comparing them with existing algorithms in various situations. Experimental results indicate that our proposed methods (CGD and CDOE) outperform their conventional counterparts (GD and DOE), especially when faced with external acceleration and magnetic disturbances. Furthermore, the new algorithms demonstrate significantly lower computational complexity than Kalman filter-based approaches, making them suitable for applications with low-cost microprocessors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge