Multi-Agent Coordination in Adversarial Environments through Signal Mediated Strategies
Paper and Code
Feb 09, 2021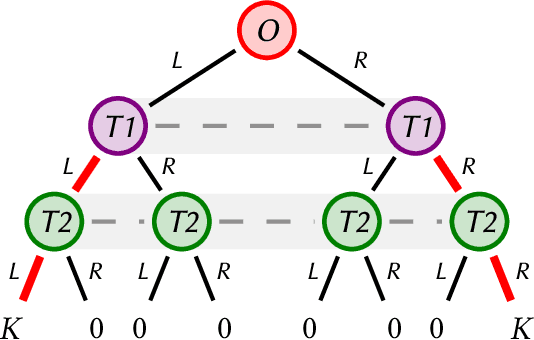
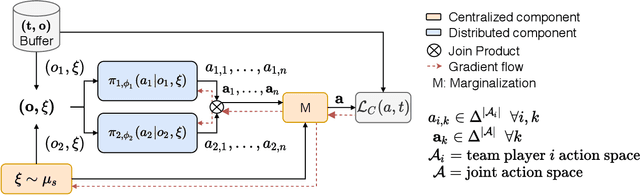
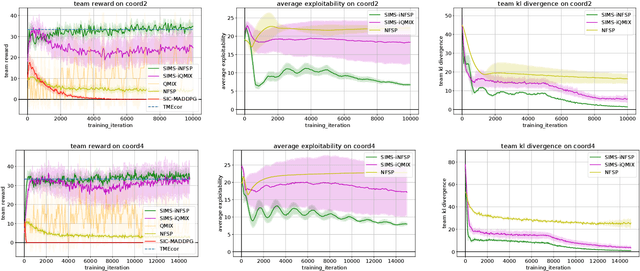

Many real-world scenarios involve teams of agents that have to coordinate their actions to reach a shared goal. We focus on the setting in which a team of agents faces an opponent in a zero-sum, imperfect-information game. Team members can coordinate their strategies before the beginning of the game, but are unable to communicate during the playing phase of the game. This is the case, for example, in Bridge, collusion in poker, and collusion in bidding. In this setting, model-free RL methods are oftentimes unable to capture coordination because agents' policies are executed in a decentralized fashion. Our first contribution is a game-theoretic centralized training regimen to effectively perform trajectory sampling so as to foster team coordination. When team members can observe each other actions, we show that this approach provably yields equilibrium strategies. Then, we introduce a signaling-based framework to represent team coordinated strategies given a buffer of past experiences. Each team member's policy is parametrized as a neural network whose output is conditioned on a suitable exogenous signal, drawn from a learned probability distribution. By combining these two elements, we empirically show convergence to coordinated equilibria in cases where previous state-of-the-art multi-agent RL algorithms did not.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge