Motion Prediction Under Multimodality with Conditional Stochastic Networks
Paper and Code
May 05, 2017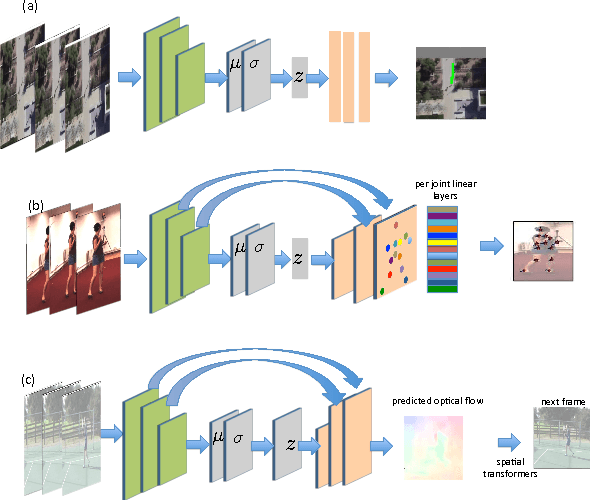
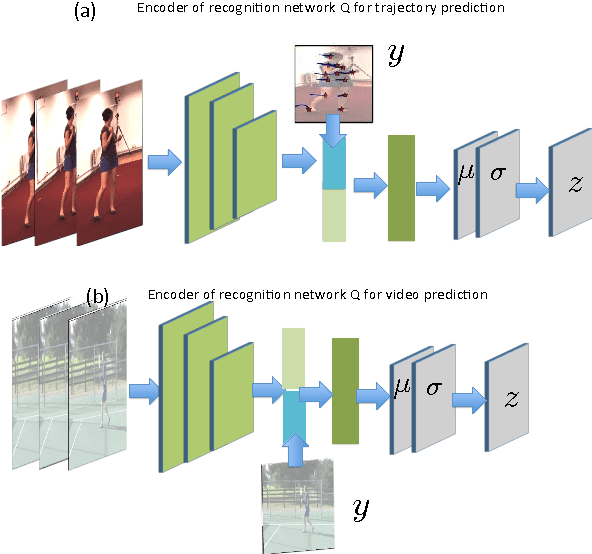

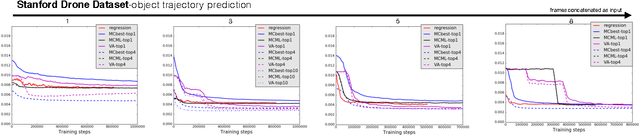
Given a visual history, multiple future outcomes for a video scene are equally probable, in other words, the distribution of future outcomes has multiple modes. Multimodality is notoriously hard to handle by standard regressors or classifiers: the former regress to the mean and the latter discretize a continuous high dimensional output space. In this work, we present stochastic neural network architectures that handle such multimodality through stochasticity: future trajectories of objects, body joints or frames are represented as deep, non-linear transformations of random (as opposed to deterministic) variables. Such random variables are sampled from simple Gaussian distributions whose means and variances are parametrized by the output of convolutional encoders over the visual history. We introduce novel convolutional architectures for predicting future body joint trajectories that outperform fully connected alternatives \cite{DBLP:journals/corr/WalkerDGH16}. We introduce stochastic spatial transformers through optical flow warping for predicting future frames, which outperform their deterministic equivalents \cite{DBLP:journals/corr/PatrauceanHC15}. Training stochastic networks involves an intractable marginalization over stochastic variables. We compare various training schemes that handle such marginalization through a) straightforward sampling from the prior, b) conditional variational autoencoders \cite{NIPS2015_5775,DBLP:journals/corr/WalkerDGH16}, and, c) a proposed K-best-sample loss that penalizes the best prediction under a fixed "prediction budget". We show experimental results on object trajectory prediction, human body joint trajectory prediction and video prediction under varying future uncertainty, validating quantitatively and qualitatively our architectural choices and training schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge