Modified Meta-Thompson Sampling for Linear Bandits and Its Bayes Regret Analysis
Paper and Code
Sep 11, 2024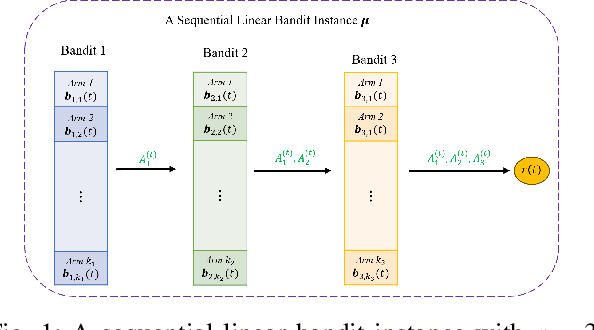
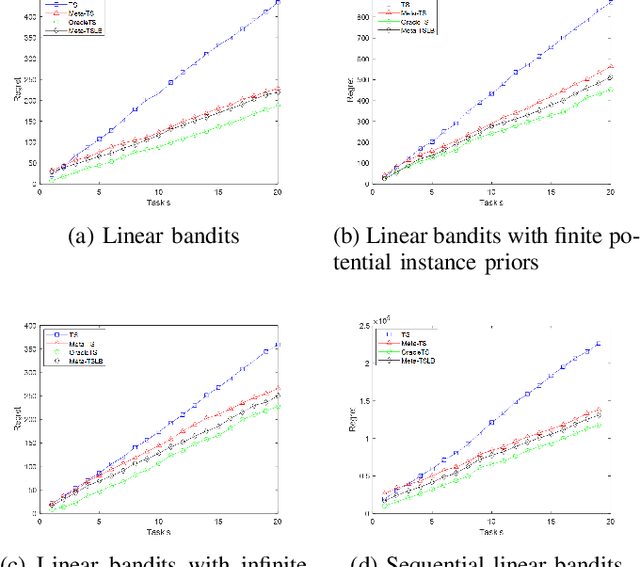
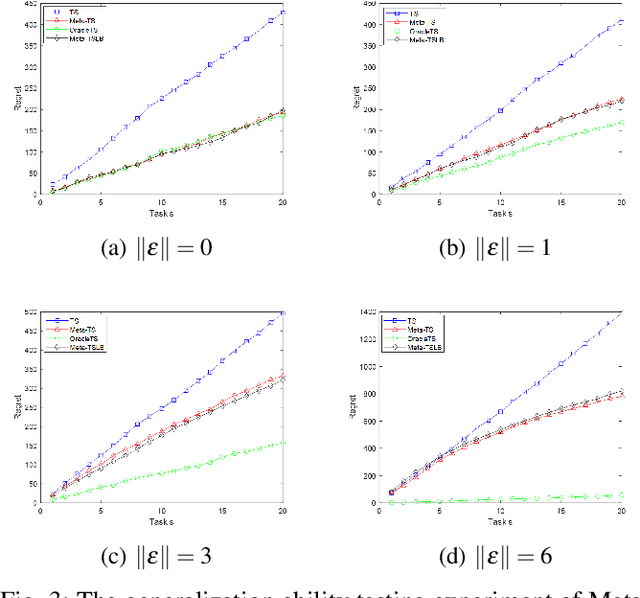
Meta-learning is characterized by its ability to learn how to learn, enabling the adaptation of learning strategies across different tasks. Recent research introduced the Meta-Thompson Sampling (Meta-TS), which meta-learns an unknown prior distribution sampled from a meta-prior by interacting with bandit instances drawn from it. However, its analysis was limited to Gaussian bandit. The contextual multi-armed bandit framework is an extension of the Gaussian Bandit, which challenges agent to utilize context vectors to predict the most valuable arms, optimally balancing exploration and exploitation to minimize regret over time. This paper introduces Meta-TSLB algorithm, a modified Meta-TS for linear contextual bandits. We theoretically analyze Meta-TSLB and derive an $ O((m+\log(m))\sqrt{n\log(n)})$ bound on its Bayes regret, in which $m$ represents the number of bandit instances, and $n$ the number of rounds of Thompson Sampling. Additionally, our work complements the analysis of Meta-TS for linear contextual bandits. The performance of Meta-TSLB is evaluated experimentally under different settings, and we experimente and analyze the generalization capability of Meta-TSLB, showcasing its potential to adapt to unseen instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge