Modeling the Data-Generating Process is Necessary for Out-of-Distribution Generalization
Paper and Code
Jun 15, 2022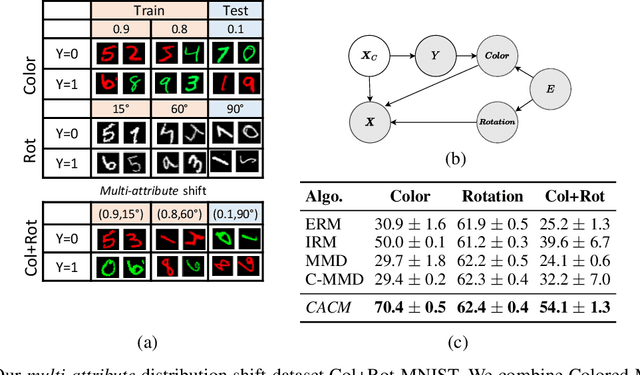

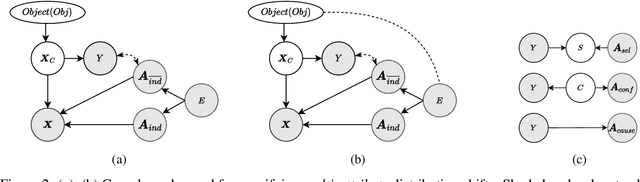
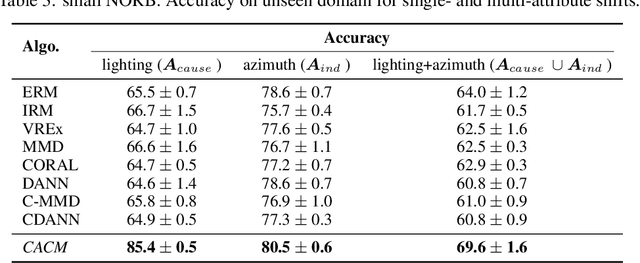
Real-world data collected from multiple domains can have multiple, distinct distribution shifts over multiple attributes. However, state-of-the art advances in domain generalization (DG) algorithms focus only on specific shifts over a single attribute. We introduce datasets with multi-attribute distribution shifts and find that existing DG algorithms fail to generalize. To explain this, we use causal graphs to characterize the different types of shifts based on the relationship between spurious attributes and the classification label. Each multi-attribute causal graph entails different constraints over observed variables, and therefore any algorithm based on a single, fixed independence constraint cannot work well across all shifts. We present Causally Adaptive Constraint Minimization (CACM), a new algorithm for identifying the correct independence constraints for regularization. Results on fully synthetic, MNIST and small NORB datasets, covering binary and multi-valued attributes and labels, confirm our theoretical claim: correct independence constraints lead to the highest accuracy on unseen domains whereas incorrect constraints fail to do so. Our results demonstrate the importance of modeling the causal relationships inherent in the data-generating process: in many cases, it is impossible to know the correct regularization constraints without this information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge