Modeling Latent Variable Uncertainty for Loss-based Learning
Paper and Code
Jun 18, 2012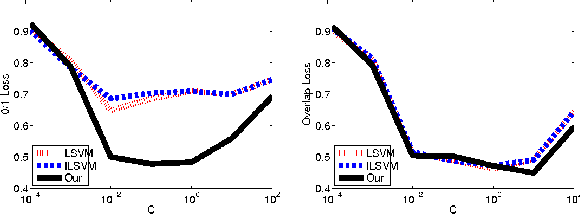
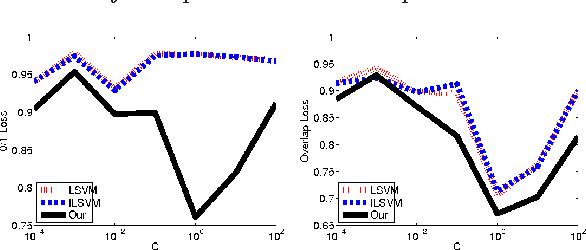
We consider the problem of parameter estimation using weakly supervised datasets, where a training sample consists of the input and a partially specified annotation, which we refer to as the output. The missing information in the annotation is modeled using latent variables. Previous methods overburden a single distribution with two separate tasks: (i) modeling the uncertainty in the latent variables during training; and (ii) making accurate predictions for the output and the latent variables during testing. We propose a novel framework that separates the demands of the two tasks using two distributions: (i) a conditional distribution to model the uncertainty of the latent variables for a given input-output pair; and (ii) a delta distribution to predict the output and the latent variables for a given input. During learning, we encourage agreement between the two distributions by minimizing a loss-based dissimilarity coefficient. Our approach generalizes latent SVM in two important ways: (i) it models the uncertainty over latent variables instead of relying on a pointwise estimate; and (ii) it allows the use of loss functions that depend on latent variables, which greatly increases its applicability. We demonstrate the efficacy of our approach on two challenging problems---object detection and action detection---using publicly available datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge