Modeling Generalization in Machine Learning: A Methodological and Computational Study
Paper and Code
Jun 28, 2020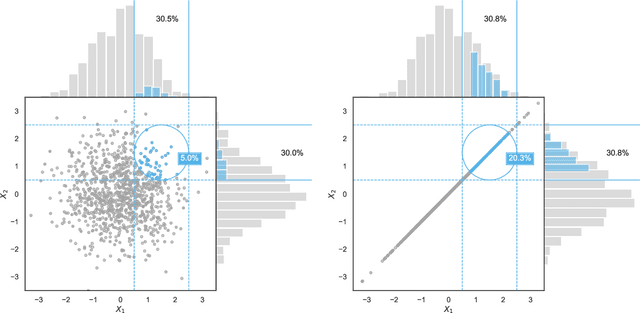
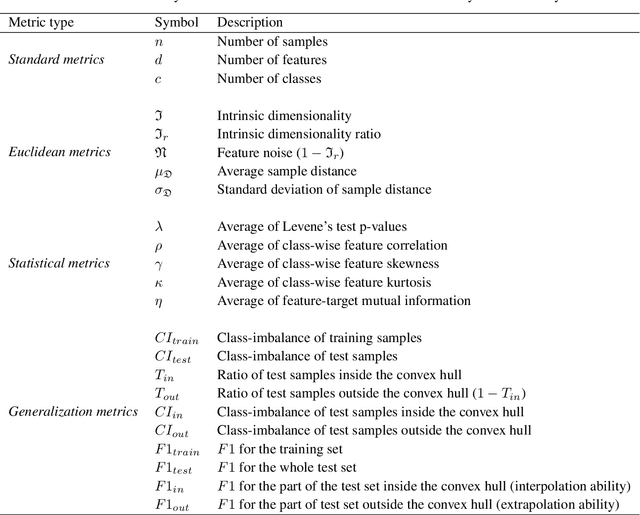
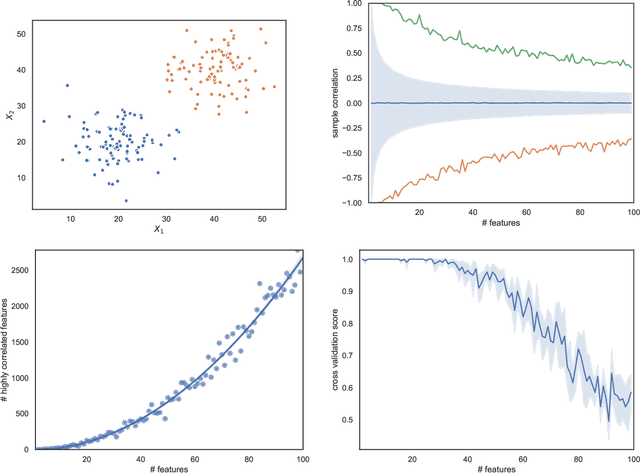
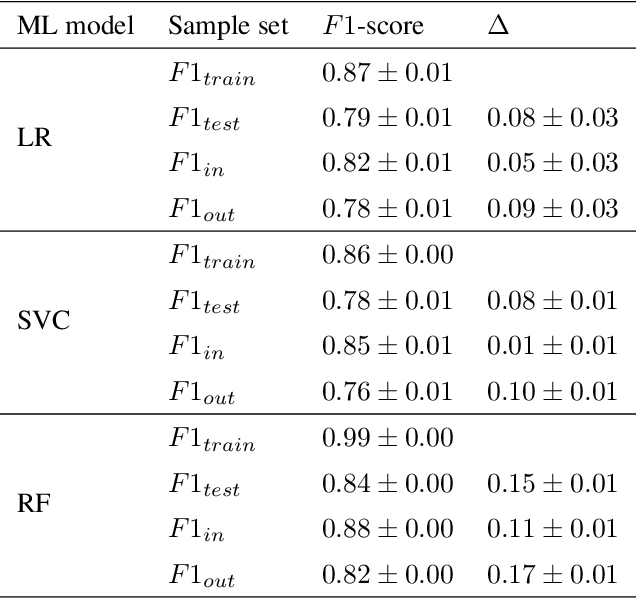
As machine learning becomes more and more available to the general public, theoretical questions are turning into pressing practical issues. Possibly, one of the most relevant concerns is the assessment of our confidence in trusting machine learning predictions. In many real-world cases, it is of utmost importance to estimate the capabilities of a machine learning algorithm to generalize, i.e., to provide accurate predictions on unseen data, depending on the characteristics of the target problem. In this work, we perform a meta-analysis of 109 publicly-available classification data sets, modeling machine learning generalization as a function of a variety of data set characteristics, ranging from number of samples to intrinsic dimensionality, from class-wise feature skewness to $F1$ evaluated on test samples falling outside the convex hull of the training set. Experimental results demonstrate the relevance of using the concept of the convex hull of the training data in assessing machine learning generalization, by emphasizing the difference between interpolated and extrapolated predictions. Besides several predictable correlations, we observe unexpectedly weak associations between the generalization ability of machine learning models and all metrics related to dimensionality, thus challenging the common assumption that the \textit{curse of dimensionality} might impair generalization in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge