MMES: Mixture Model based Evolution Strategy for Large-Scale Optimization
Paper and Code
Mar 15, 2022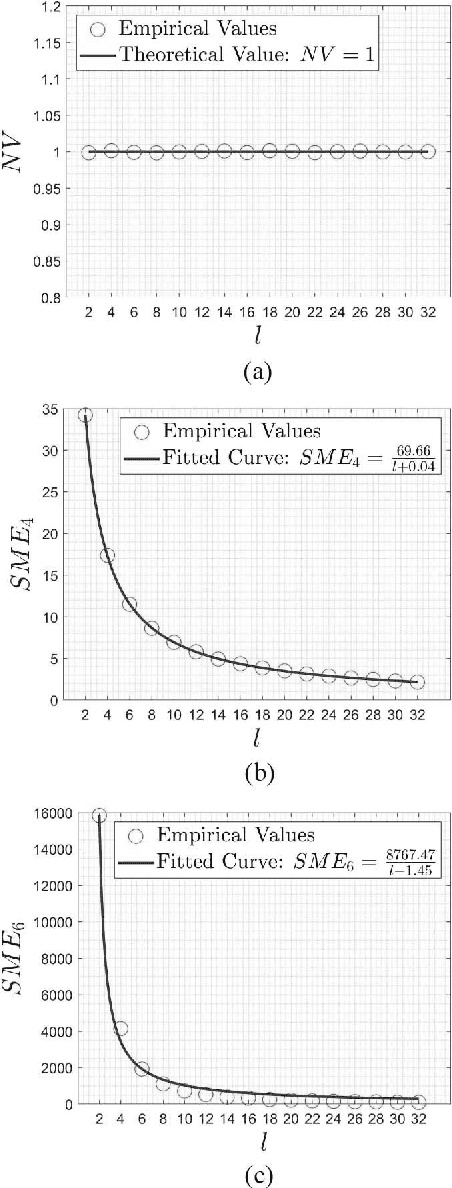
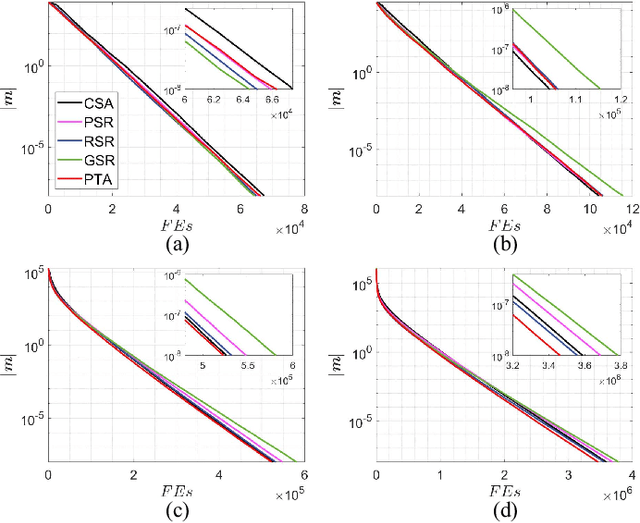
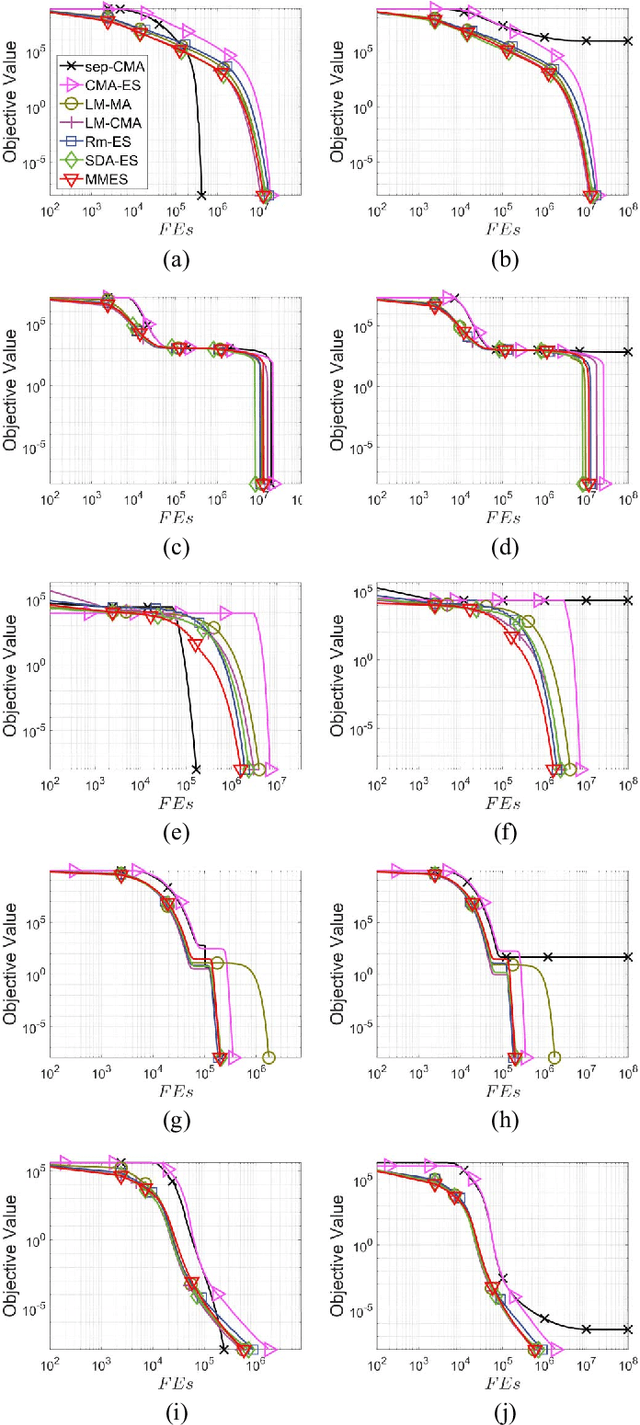

This work provides an efficient sampling method for the covariance matrix adaptation evolution strategy (CMA-ES) in large-scale settings. In contract to the Gaussian sampling in CMA-ES, the proposed method generates mutation vectors from a mixture model, which facilitates exploiting the rich variable correlations of the problem landscape within a limited time budget. We analyze the probability distribution of this mixture model and show that it approximates the Gaussian distribution of CMA-ES with a controllable accuracy. We use this sampling method, coupled with a novel method for mutation strength adaptation, to formulate the mixture model based evolution strategy (MMES) -- a CMA-ES variant for large-scale optimization. The numerical simulations show that, while significantly reducing the time complexity of CMA-ES, MMES preserves the rotational invariance, is scalable to high dimensional problems, and is competitive against the state-of-the-arts in performing global optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge