Mixed Noise Removal with Pareto Prior
Paper and Code
Aug 27, 2020


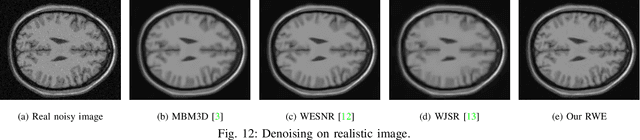
Denoising images contaminated by the mixture of additive white Gaussian noise (AWGN) and impulse noise (IN) is an essential but challenging problem. The presence of impulsive disturbances inevitably affects the distribution of noises and thus largely degrades the performance of traditional AWGN denoisers. Existing methods target to compensate the effects of IN by introducing a weighting matrix, which, however, is lack of proper priori and thus hard to be accurately estimated. To address this problem, we exploit the Pareto distribution as the priori of the weighting matrix, based on which an accurate and robust weight estimator is proposed for mixed noise removal. Particularly, a relatively small portion of pixels are assumed to be contaminated with IN, which should have weights with small values and then be penalized out. This phenomenon can be properly described by the Pareto distribution of type 1. Therefore, armed with the Pareto distribution, we formulate the problem of mixed noise removal in the Bayesian framework, where nonlocal self-similarity priori is further exploited by adopting nonlocal low rank approximation. Compared to existing methods, the proposed method can estimate the weighting matrix adaptively, accurately, and robust for different level of noises, thus can boost the denoising performance. Experimental results on widely used image datasets demonstrate the superiority of our proposed method to the state-of-the-arts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge