Mitigating Overfitting in Supervised Classification from Two Unlabeled Datasets: A Consistent Risk Correction Approach
Paper and Code
Oct 20, 2019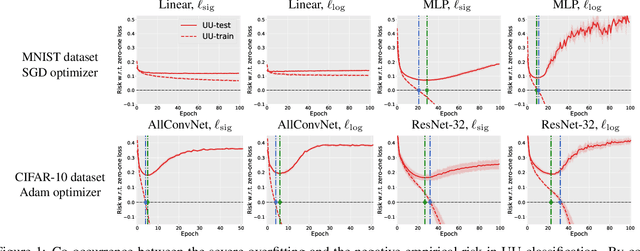
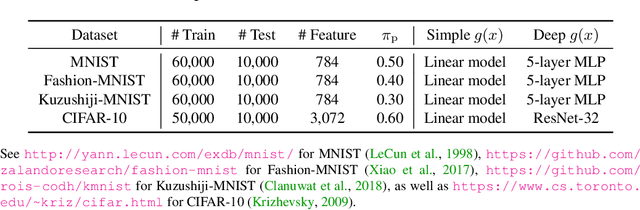
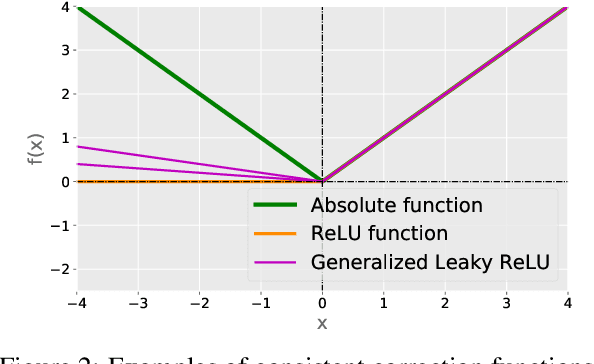
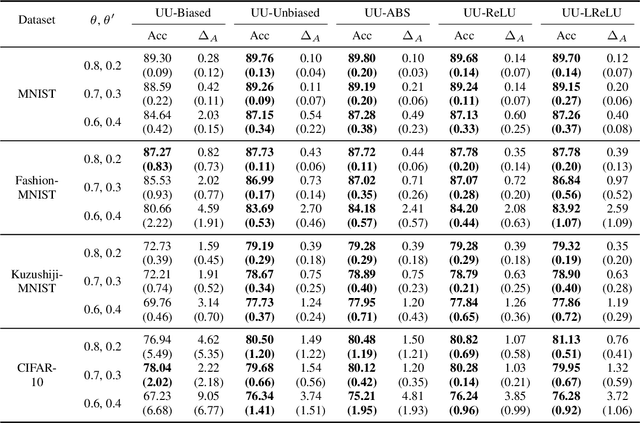
From two unlabeled (U) datasets with different class priors, we can train a binary classifier by empirical risk minimization, which is called UU classification. It is promising since UU methods are compatible with any neural network (NN) architecture and optimizer as if it is standard supervised classification. In this paper, however, we find that UU methods may suffer severe overfitting, and there is a high co-occurrence between the overfitting and the negative empirical risk regardless of datasets, NN architectures, and optimizers. Hence, to mitigate the overfitting problem of UU methods, we propose to keep two parts of the empirical risk (i.e., false positive and false negative) non-negative by wrapping them in a family of correction functions. We theoretically show that the corrected risk estimator is still asymptotically unbiased and consistent; furthermore we establish an estimation error bound for the corrected risk minimizer. Experiments with feedforward/residual NNs on standard benchmarks demonstrate that our proposed correction can successfully mitigate the overfitting of UU methods and significantly improve the classification accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge