Minimax in Geodesic Metric Spaces: Sion's Theorem and Algorithms
Paper and Code
Feb 13, 2022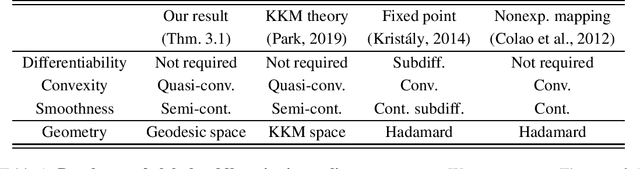
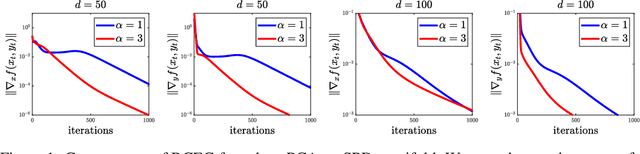

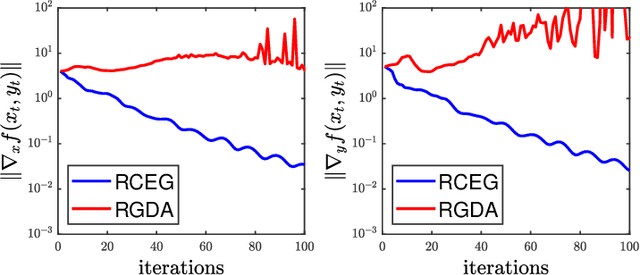
Determining whether saddle points exist or are approximable for nonconvex-nonconcave problems is usually intractable. We take a step towards understanding certain nonconvex-nonconcave minimax problems that do remain tractable. Specifically, we study minimax problems cast in geodesic metric spaces, which provide a vast generalization of the usual convex-concave saddle point problems. The first main result of the paper is a geodesic metric space version of Sion's minimax theorem; we believe our proof is novel and transparent, as it relies on Helly's theorem only. In our second main result, we specialize to geodesically complete Riemannian manifolds: we devise and analyze the complexity of first-order methods for smooth minimax problems.
* 19 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge