metricDTW: local distance metric learning in Dynamic Time Warping
Paper and Code
Jun 11, 2016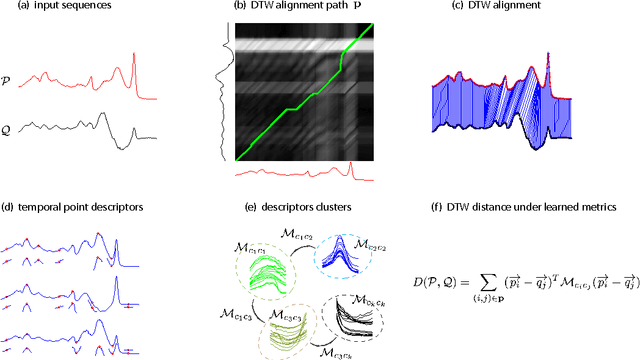
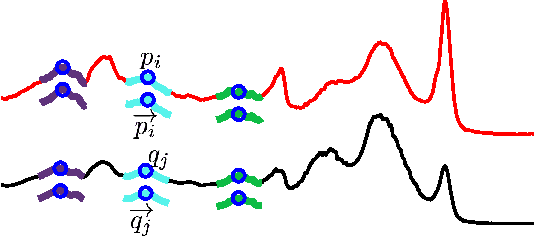
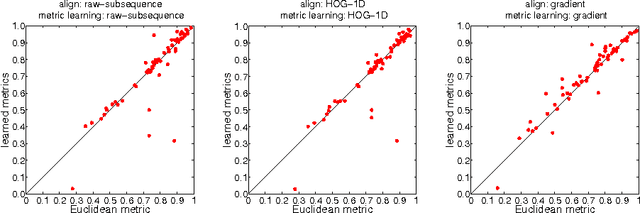
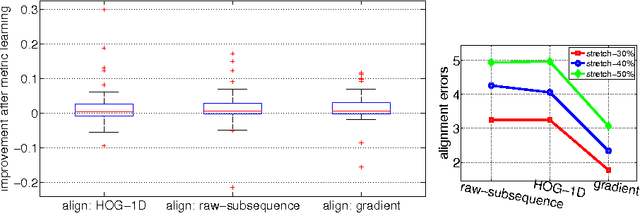
We propose to learn multiple local Mahalanobis distance metrics to perform k-nearest neighbor (kNN) classification of temporal sequences. Temporal sequences are first aligned by dynamic time warping (DTW); given the alignment path, similarity between two sequences is measured by the DTW distance, which is computed as the accumulated distance between matched temporal point pairs along the alignment path. Traditionally, Euclidean metric is used for distance computation between matched pairs, which ignores the data regularities and might not be optimal for applications at hand. Here we propose to learn multiple Mahalanobis metrics, such that DTW distance becomes the sum of Mahalanobis distances. We adapt the large margin nearest neighbor (LMNN) framework to our case, and formulate multiple metric learning as a linear programming problem. Extensive sequence classification results show that our proposed multiple metrics learning approach is effective, insensitive to the preceding alignment qualities, and reaches the state-of-the-art performances on UCR time series datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge