Meta Mirror Descent: Optimiser Learning for Fast Convergence
Paper and Code
Mar 05, 2022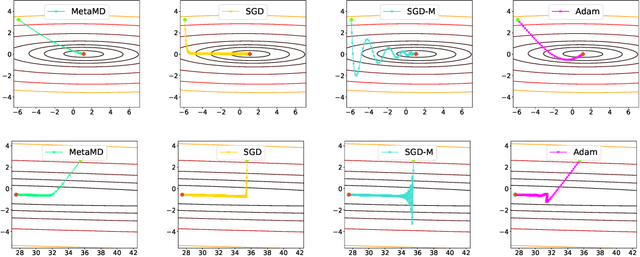
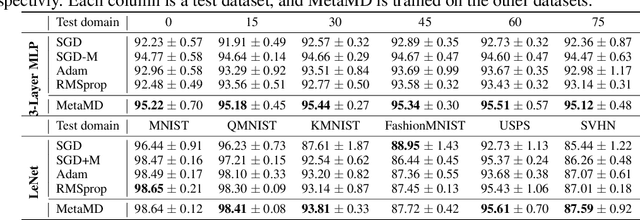
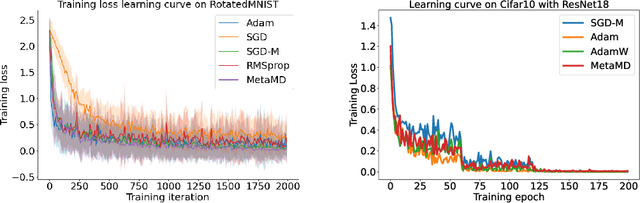
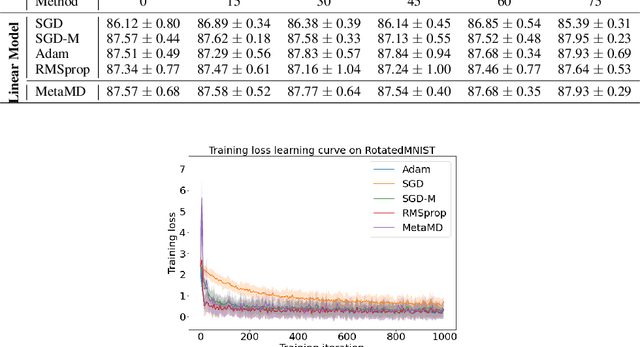
Optimisers are an essential component for training machine learning models, and their design influences learning speed and generalisation. Several studies have attempted to learn more effective gradient-descent optimisers via solving a bi-level optimisation problem where generalisation error is minimised with respect to optimiser parameters. However, most existing optimiser learning methods are intuitively motivated, without clear theoretical support. We take a different perspective starting from mirror descent rather than gradient descent, and meta-learning the corresponding Bregman divergence. Within this paradigm, we formalise a novel meta-learning objective of minimising the regret bound of learning. The resulting framework, termed Meta Mirror Descent (MetaMD), learns to accelerate optimisation speed. Unlike many meta-learned optimisers, it also supports convergence and generalisation guarantees and uniquely does so without requiring validation data. We evaluate our framework on a variety of tasks and architectures in terms of convergence rate and generalisation error and demonstrate strong performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge