Meta-Learning from Learning Curves for Budget-Limited Algorithm Selection
Paper and Code
Oct 10, 2024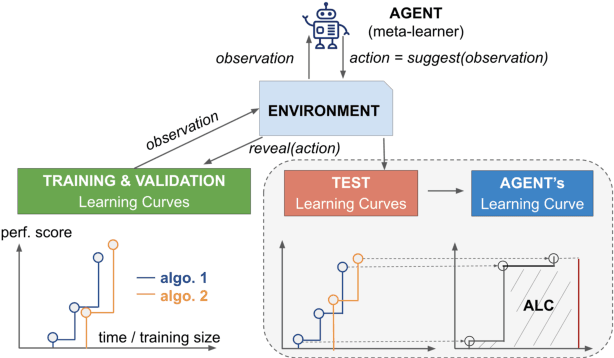
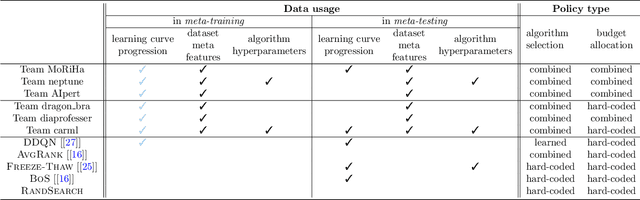
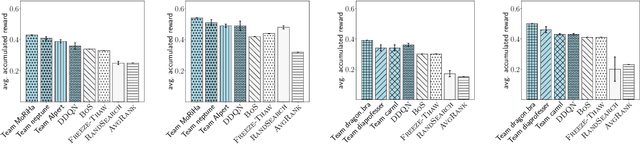
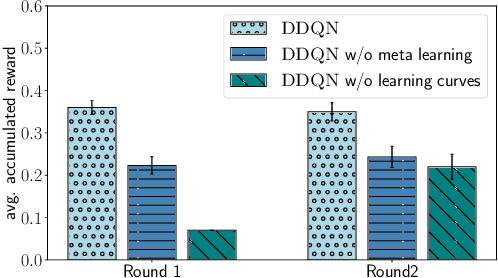
Training a large set of machine learning algorithms to convergence in order to select the best-performing algorithm for a dataset is computationally wasteful. Moreover, in a budget-limited scenario, it is crucial to carefully select an algorithm candidate and allocate a budget for training it, ensuring that the limited budget is optimally distributed to favor the most promising candidates. Casting this problem as a Markov Decision Process, we propose a novel framework in which an agent must select in the process of learning the most promising algorithm without waiting until it is fully trained. At each time step, given an observation of partial learning curves of algorithms, the agent must decide whether to allocate resources to further train the most promising algorithm (exploitation), to wake up another algorithm previously put to sleep, or to start training a new algorithm (exploration). In addition, our framework allows the agent to meta-learn from learning curves on past datasets along with dataset meta-features and algorithm hyperparameters. By incorporating meta-learning, we aim to avoid myopic decisions based solely on premature learning curves on the dataset at hand. We introduce two benchmarks of learning curves that served in international competitions at WCCI'22 and AutoML-conf'22, of which we analyze the results. Our findings show that both meta-learning and the progression of learning curves enhance the algorithm selection process, as evidenced by methods of winning teams and our DDQN baseline, compared to heuristic baselines or a random search. Interestingly, our cost-effective baseline, which selects the best-performing algorithm w.r.t. a small budget, can perform decently when learning curves do not intersect frequently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge