Meta-Learning for Relative Density-Ratio Estimation
Paper and Code
Jul 02, 2021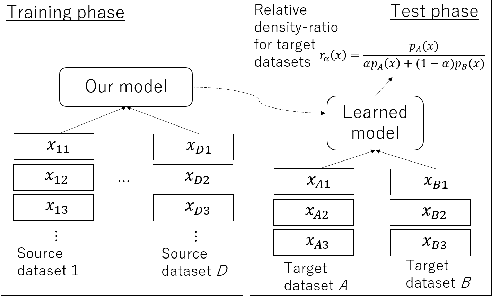
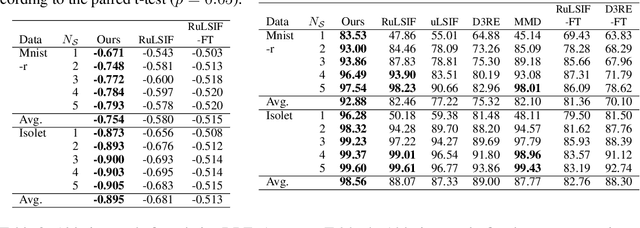

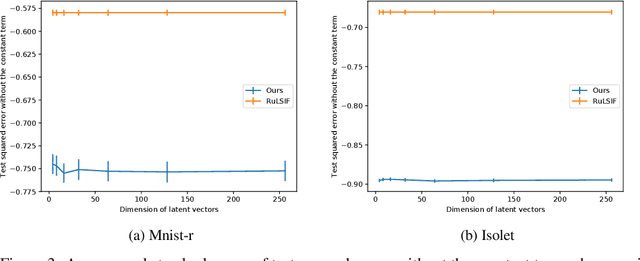
The ratio of two probability densities, called a density-ratio, is a vital quantity in machine learning. In particular, a relative density-ratio, which is a bounded extension of the density-ratio, has received much attention due to its stability and has been used in various applications such as outlier detection and dataset comparison. Existing methods for (relative) density-ratio estimation (DRE) require many instances from both densities. However, sufficient instances are often unavailable in practice. In this paper, we propose a meta-learning method for relative DRE, which estimates the relative density-ratio from a few instances by using knowledge in related datasets. Specifically, given two datasets that consist of a few instances, our model extracts the datasets' information by using neural networks and uses it to obtain instance embeddings appropriate for the relative DRE. We model the relative density-ratio by a linear model on the embedded space, whose global optimum solution can be obtained as a closed-form solution. The closed-form solution enables fast and effective adaptation to a few instances, and its differentiability enables us to train our model such that the expected test error for relative DRE can be explicitly minimized after adapting to a few instances. We empirically demonstrate the effectiveness of the proposed method by using three problems: relative DRE, dataset comparison, and outlier detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge