Meta-Cognition. An Inverse-Inverse Reinforcement Learning Approach for Cognitive Radars

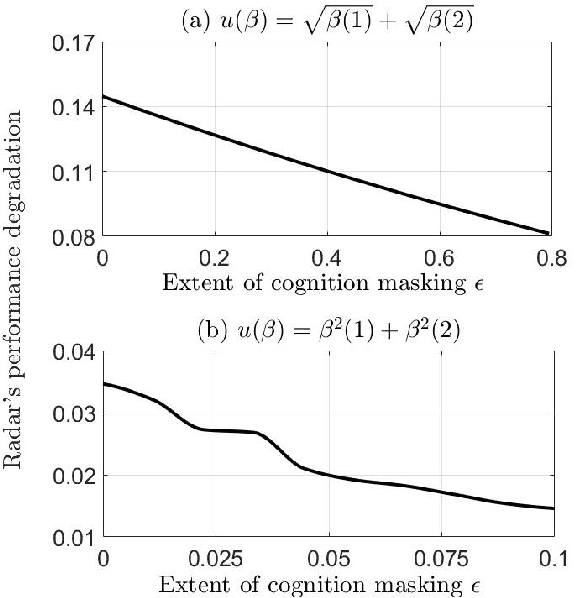
This paper considers meta-cognitive radars in an adversarial setting. A cognitive radar optimally adapts its waveform (response) in response to maneuvers (probes) of a possibly adversarial moving target. A meta-cognitive radar is aware of the adversarial nature of the target and seeks to mitigate the adversarial target. How should the meta-cognitive radar choose its responses to sufficiently confuse the adversary trying to estimate the radar's utility function? This paper abstracts the radar's meta-cognition problem in terms of the spectra (eigenvalues) of the state and observation noise covariance matrices, and embeds the algebraic Riccati equation into an economics-based utility maximization setup. This adversarial target is an inverse reinforcement learner. By observing a noisy sequence of radar's responses (waveforms), the adversarial target uses a statistical hypothesis test to detect if the radar is a utility maximizer. In turn, the meta-cognitive radar deliberately chooses sub-optimal responses that increasing its Type-I error probability of the adversary's detector. We call this counter-adversarial step taken by the meta-cognitive radar as inverse inverse reinforcement learning (I-IRL). We illustrate the meta-cognition results of this paper via simple numerical examples. Our approach for meta-cognition in this paper is based on revealed preference theory in micro-economics and inspired by results in differential privacy and adversarial obfuscation in machine learning.