Memory AMP for Generalized MIMO: Coding Principle and Information-Theoretic Optimality
Paper and Code
Nov 07, 2023
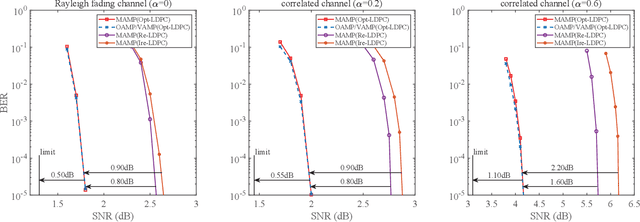
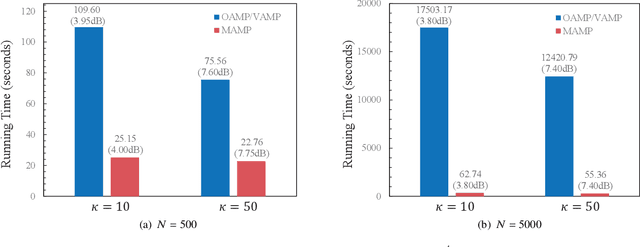
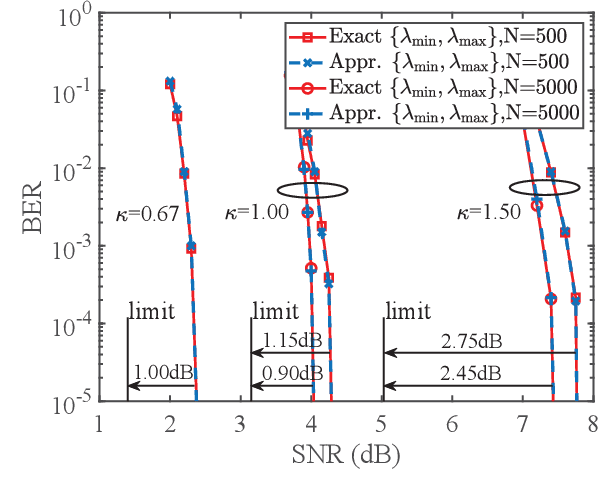
To support complex communication scenarios in next-generation wireless communications, this paper focuses on a generalized MIMO (GMIMO) with practical assumptions, such as massive antennas, practical channel coding, arbitrary input distributions, and general right-unitarily-invariant channel matrices (covering Rayleigh fading, certain ill-conditioned and correlated channel matrices). The orthogonal/vector approximate message passing (OAMP/VAMP) receiver has been proved to be information-theoretically optimal in GMIMO, but it is limited to high-complexity LMMSE. To solve this problem, a low-complexity memory approximate message passing (MAMP) receiver has recently been shown to be Bayes optimal but limited to uncoded systems. Therefore, how to design a low-complexity and information-theoretically optimal receiver for GMIMO is still an open issue. To address this issue, this paper proposes an information-theoretically optimal MAMP receiver and investigates its achievable rate analysis and optimal coding principle. Specifically, due to the long-memory linear detection, state evolution (SE) for MAMP is intricately multidimensional and cannot be used directly to analyze its achievable rate. To avoid this difficulty, a simplified single-input single-output variational SE (VSE) for MAMP is developed by leveraging the SE fixed-point consistent property of MAMP and OAMP/VAMP. The achievable rate of MAMP is calculated using the VSE, and the optimal coding principle is established to maximize the achievable rate. On this basis, the information-theoretic optimality of MAMP is proved rigorously. Numerical results show that the finite-length performances of MAMP with practical optimized LDPC codes are 0.5-2.7 dB away from the associated constrained capacities. It is worth noting that MAMP can achieve the same performances as OAMP/VAMP with 0.4% of the time consumption for large-scale systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge