Mechanics-based Analysis on Flagellated Robots
Paper and Code
Dec 27, 2021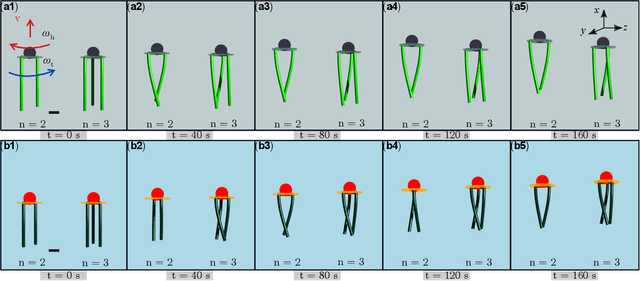
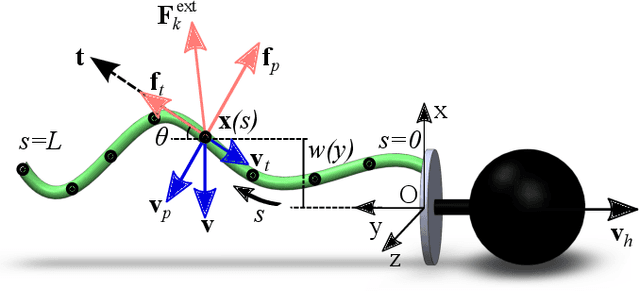

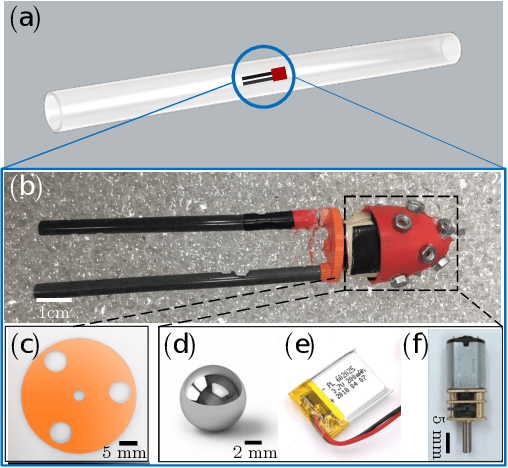
We explore the locomotion of soft robots in granular medium (GM) resulting from the elastic deformation of slender rods. A low-cost, rapidly fabricable robot inspired by the physiological structure of bacteria is presented. It consists of a rigid head, with a motor and batteries embedded, and multiple elastic rods (our model for flagella) to investigate locomotion in GM. The elastic flagella are rotated at one end by the motor, and they deform due to the drag from GM, propelling the robot. The external drag is determined by the flagellar shape, while the latter changes due to the competition between external loading and elastic forces. In this coupled fluid-structure interaction problem, we observe that increasing the number of flagella can decrease or increase the propulsive speed of the robot, depending on the physical parameters of the system. This nonlinearity in the functional relation between propulsion and the parameters of this simple robot motivates us to fundamentally analyze its mechanics using theory, numerical simulation, and experiments. We present a simple Euler-Bernoulli beam theory-based analytical framework that is capable of qualitatively capturing both cases. Theoretical prediction quantitatively matches experiments when the flagellar deformation is small. To account for the geometrically nonlinear deformation often encountered in soft robots and microbes, we implement a simulation framework that incorporates discrete differential geometry-based simulations of elastic rods, a resistive force theory-based model for drag, and a modified Stokes law for the hydrodynamics of the robot head. Comparison with experimental data indicates that the simulations can quantitatively predict robotic motion. Overall, the theoretical and numerical tools presented in this paper can shed light on the design and control of this class of articulated robots in granular or fluid media.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge