Maxmin Q-learning: Controlling the Estimation Bias of Q-learning
Paper and Code
Feb 16, 2020


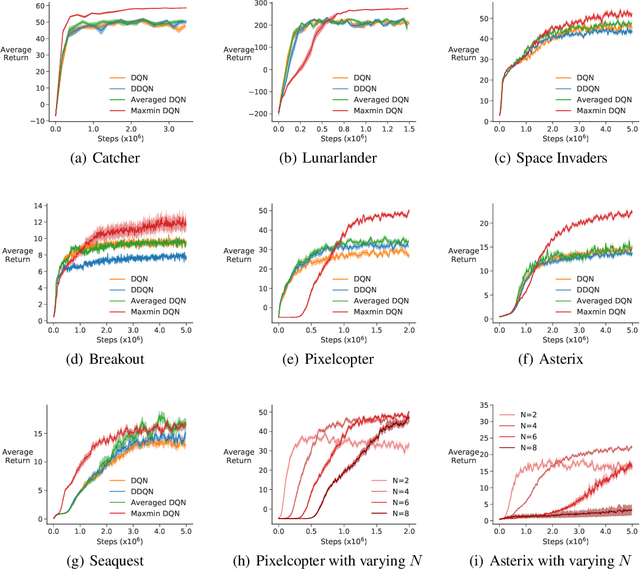
Q-learning suffers from overestimation bias, because it approximates the maximum action value using the maximum estimated action value. Algorithms have been proposed to reduce overestimation bias, but we lack an understanding of how bias interacts with performance, and the extent to which existing algorithms mitigate bias. In this paper, we 1) highlight that the effect of overestimation bias on learning efficiency is environment-dependent; 2) propose a generalization of Q-learning, called \emph{Maxmin Q-learning}, which provides a parameter to flexibly control bias; 3) show theoretically that there exists a parameter choice for Maxmin Q-learning that leads to unbiased estimation with a lower approximation variance than Q-learning; and 4) prove the convergence of our algorithm in the tabular case, as well as convergence of several previous Q-learning variants, using a novel Generalized Q-learning framework. We empirically verify that our algorithm better controls estimation bias in toy environments, and that it achieves superior performance on several benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge