Margin-Based Transfer Bounds for Meta Learning with Deep Feature Embedding
Paper and Code
Dec 02, 2020
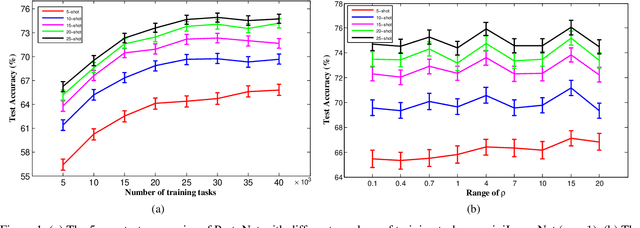

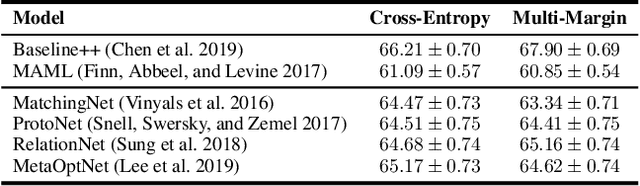
By transferring knowledge learned from seen/previous tasks, meta learning aims to generalize well to unseen/future tasks. Existing meta-learning approaches have shown promising empirical performance on various multiclass classification problems, but few provide theoretical analysis on the classifiers' generalization ability on future tasks. In this paper, under the assumption that all classification tasks are sampled from the same meta-distribution, we leverage margin theory and statistical learning theory to establish three margin-based transfer bounds for meta-learning based multiclass classification (MLMC). These bounds reveal that the expected error of a given classification algorithm for a future task can be estimated with the average empirical error on a finite number of previous tasks, uniformly over a class of preprocessing feature maps/deep neural networks (i.e. deep feature embeddings). To validate these bounds, instead of the commonly-used cross-entropy loss, a multi-margin loss is employed to train a number of representative MLMC models. Experiments on three benchmarks show that these margin-based models still achieve competitive performance, validating the practical value of our margin-based theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge