Manipulability Maximization Using Continuous-Time Gaussian Processes
Paper and Code
Sep 11, 2018
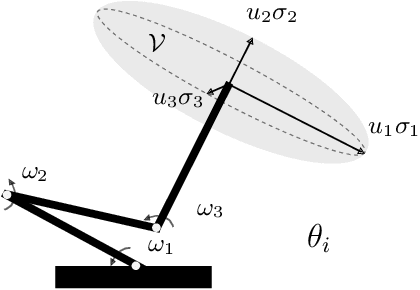
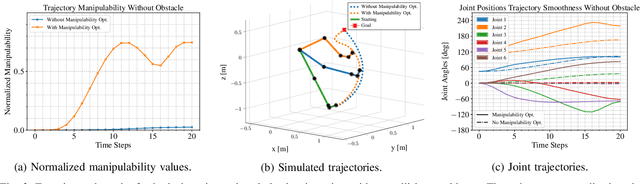
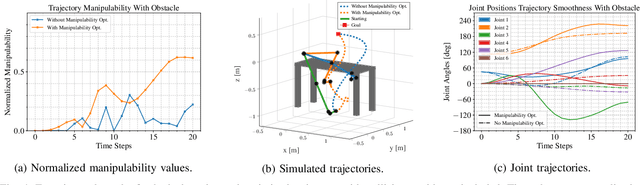
A significant challenge in motion planning is to avoid being in or near \emph{singular configurations} (\textit{singularities}), that is, joint configurations that result in the loss of the ability to move in certain directions in task space. A robotic system's capacity for motion is reduced even in regions that are in close proximity to (i.e., neighbouring) a singularity. In this work we examine singularity avoidance in a motion planning context, finding trajectories which minimize proximity to singular regions, subject to constraints. We define a manipulability-based likelihood associated with singularity avoidance over a continuous trajectory representation, which we then maximize using a \textit{maximum a posteriori} (MAP) estimator. Viewing the MAP problem as inference on a factor graph, we use gradient information from interpolated states to maximize the trajectory's overall manipulability. Both qualitative and quantitative analyses of experimental data show increases in manipulability that result in smooth trajectories with visibly more dexterous arm configurations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge